Sample covariance matrix
Definition
For a vector ![]() , the sample variance
, the sample variance ![]() measures the average deviation of its coefficients around the sample average
measures the average deviation of its coefficients around the sample average ![]() :
:
Now consider a matrix ![]() , where each column
, where each column ![]() represents a data point in
represents a data point in ![]() . We are interested in describing the amount of variance in this data set. To this end, we look at the numbers we obtain by projecting the data along a line defined by the direction
. We are interested in describing the amount of variance in this data set. To this end, we look at the numbers we obtain by projecting the data along a line defined by the direction ![]() . This corresponds to the (row) vector in
. This corresponds to the (row) vector in ![]() .
.
The corresponding sample mean and variance are
where ![]() is the sample mean of the vectors
is the sample mean of the vectors ![]() .
.
The sample variance along direction ![]() can be expressed as a quadratic form in
can be expressed as a quadratic form in ![]() :
:
where ![]() is a
is a ![]() symmetric matrix, called the sample covariance matrix of the data points:
symmetric matrix, called the sample covariance matrix of the data points:
Properties
The covariance matrix satisfies the following properties.
- The sample covariance matrix allows finding the variance along any direction in data space.
- The diagonal elements of
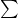 give the variances of each vector in the data.
give the variances of each vector in the data. - The trace of
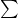 gives the sum of all the variances.
gives the sum of all the variances. - The matrix
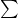 is positive semi-definite, since the associated quadratic form
is positive semi-definite, since the associated quadratic form 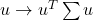 is non-negative everywhere.
is non-negative everywhere.
Matlab syntax
The following matlab syntax assumes that the ![]() data points in
data points in ![]() are collected in a
are collected in a ![]() matrix
matrix ![]() :
: ![]() .
.
>> xhat = mean(X,2); % mean of columns of matrix X >> Xc = X-xhat*ones(1,m); % centered data matrix >> Sigma = (1/m)*Xc'*Xc; % covariance matrix >> Sigma = cov(X',1); % built-in command produces the same thing
