Representation of a two-variable quadratic function
The quadratic function ![]() , with values
, with values
can be represented via a symmetric matrix, as
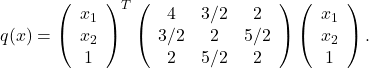
In short:
where , and
The quadratic function ![]() , with values
, with values
can be represented via a symmetric matrix, as
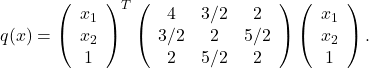
In short:
where , and