Rayleigh quotients

L. El Ghaoui

Rayleigh quotients

Theorem

Fo a symmetric matrix $A$ , we can express the smallest and largest eigenvalues, $\lambda_{\min} (A)$ and $\lambda_{\max} (A)$ , as

$\lambda_{\min}(A) = \min\limits_{x} \{x^TAx: x^Tx = 1\},$

$\lambda_{\max}(A) = \max\limits_{x} \{x^TAx: x^Tx = 1\}.$

Proof: The proof of the expression above derives from the SED of the matrix, and the invariance of the Euclidean norm constraint under orthogonal transformations. We show this only for the largest eigenvalue; the proof for the expression for the smallest eigenvalue follows similar lines. Indeed, with $A= U\Lambda U^T$ , we have

$\max\limits_{x} \{x^TAx: x^Tx = 1\} = \max\limits_{x} \{x^TU\Lambda U^Tx: x^Tx = 1\}.$

Now we can define the new variable $\tilde{x} = U^Tx$ , so that $x = U \tilde{x} = u_i$ , and express the problem as

$\max\limits_{\hat{x}} \{x^TAx: x^Tx = 1\} = \max\limits_{x} \{\hat{x}^T\Lambda \hat{x}: \hat{x}^T\hat{x} = 1\} = \max\limits_{\hat{x}}\left\{\sum\limits_{i=1}^n \lambda_i \tilde{x}_i^2: \sum\limits_{i=1}^n \tilde{x}_i^2 =1 \right\}.$

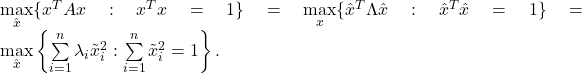
Clearly, the maximum is less than $\lambda_{\max}$ . That upper bound is attained, with $\tilde{x}_i =1$ for an index $i$ such that $\lambda_i = \lambda_{\max}$ , and $\tilde{x}_i =0$ for $j \neq i$ . This proves the result. This corresponds to setting $x = U \tilde{x} = u_i$ , where $u_i$ is the eigenvector corresponding to $\lambda_i = \lambda_{\max}$ .

Rayleigh quotients

License

Share This Book