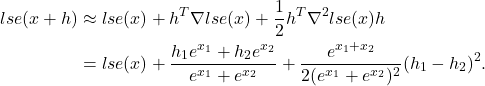Quadratic Approximation of the Log-Sum-Exp Function
As seen here, the log-sum-exp function ![]() , with values
, with values
admits the following gradient and Hessian at a point ![]() :
:
Hence, the quadratic approximation of the log-sum-exp function at a point ![]() is given by
is given by
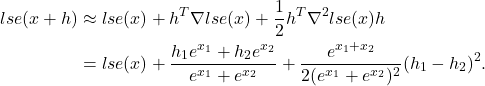
As seen here, the log-sum-exp function ![]() , with values
, with values
admits the following gradient and Hessian at a point ![]() :
:
Hence, the quadratic approximation of the log-sum-exp function at a point ![]() is given by
is given by