Pseudo-Inverse of a Matrix

L. El Ghaoui

Pseudo-Inverse of a Matrix

The pseudo-inverse of a $m \times n$ matrix $A$ is a matrix that generalizes to arbitrary matrices the notion of the inverse of a square, invertible matrix. The pseudo-inverse can be expressed from the singular value decomposition (SVD) of $A$ , as follows.

Let the SVD of $A$ be

$A=U\left(\begin{array}{ll} S & 0 \\ 0 & 0 \end{array}\right) V^T,$

where $U, V$ are both orthogonal matrices, and $S$ is a diagonal matrix containing the (positive) singular values of $A$ on its diagonal.

Then the pseudo-inverse of $A$ is the $n \times m$ matrix defined as

$A^{\dagger}=V\left(\begin{array}{cc} S^{-1} & 0 \\ 0 & 0 \end{array}\right) U^T .$

Note that $A^{\dagger}$ has the same dimension as the transpose of $A$ .

This matrix has many useful properties:

If 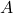$A$ is full column rank, meaning 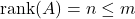$\operatorname{rank}(A)=n \leq m$ , that is, 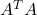$A^T A$ is not singular, then 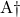$\mathrm{A} \dagger$ is a left inverse of 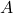$A$ , in the sense that 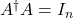$A^{\dagger} A=I_n$ . We have the closed-form expression

$A^{\dagger}=\left(A^T A\right)^{-1} A^T$

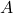If $A$ is full row rank, meaning 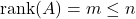$\operatorname{rank}(A)=m \leq n$ , that is, 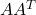$A A^T$ is not singular, then 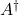$A^{\dagger}$ is a right inverse of 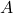$A$ , in the sense that 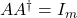$A A^{\dagger}=I_m$ . We have the closed-form expression

$A^{\dagger}=A^T\left(A A^T\right)^{-1}$

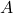If $A$ is square, invertible, then its inverse is $A^{\dagger}=A^{-1}$ .
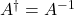The solution to the least-squares problem

$\min _x\|A x-y\|_2$

with the minimum norm is $x^*=A^{\dagger} y$ .

Example: pseudo-inverse of a 4×5 matrix.

Pseudo-Inverse of a Matrix

License

Share This Book