Pseudo-inverse of a 4 times 5 matrix via its SVD

L. El Ghaoui

Pseudo-inverse of a 4 times 5 matrix via its SVD

Returning to this example, the pseudo-inverse of the matrix

$A=\left(\begin{array}{lllll} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 & 0 \end{array}\right)$

Can be computed via an SVD: $A=U \tilde{S} V^T$ , with

$U=\left(\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 1 & 0 & 0 & 0 \end{array}\right), \tilde{S}=\left(\begin{array}{ccccc} 4 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 \\ 0 & 0 & \sqrt{5} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right), V^T=\left(\begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ \sqrt{0.2} & 0 & 0 & 0 & \sqrt{0.8} \\ 0 & 0 & 0 & 1 & 0 \\ -\sqrt{0.8} & 0 & 0 & 0 & \sqrt{0.2} \end{array}\right),$

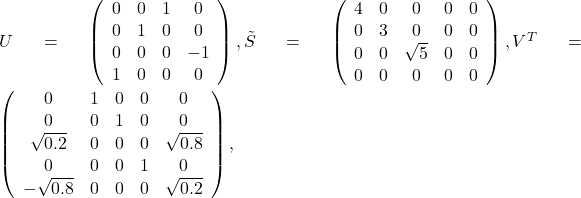
as follows.

We first invert $\tilde{S}$ , simply ‘‘inverting what can be inverted’’ and leaving zero values alone. We get

$\tilde{S}^{\dagger}=\left(\begin{array}{cccc} 1 / 4 & 0 & 0 & 0 \\ 0 & 1 / 3 & 0 & 0 \\ 0 & 0 & 1 / \sqrt{5} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right)$

Then the pseudo-inverse is obtained by exchanging the roles of $U, V$ in the SVD:

$A^{\dagger}=V \tilde{S}^{\dagger} U^T=\left(\begin{array}{cccc} 0.2000 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0.2500 \\ 0 & 0.3333 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0.4000 & 0 & 0 & 0 \end{array}\right) .$

See also: this example.

Pseudo-inverse of a 4 times 5 matrix via its SVD

License

Share This Book