Projection on a line

L. El Ghaoui

Projection on a line

Definition
Closed-form expression
Interpreting the scalar product

Definition

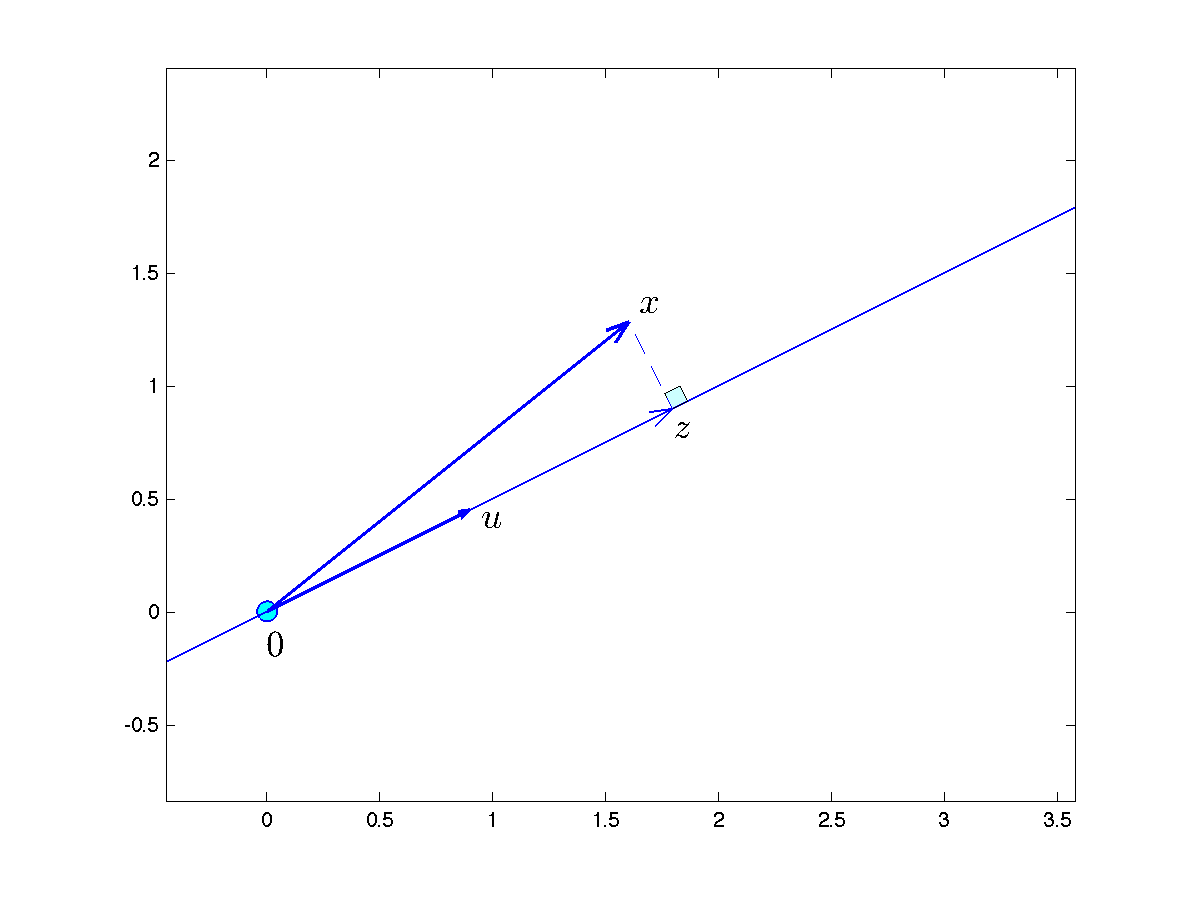
Consider the line in $\mathbb{R}^n$ passing through $x_0 \in \mathbb{R}^n$ and with direction $u \in \mathbb{R}^n$ :

${x_0 + tu: t \in \mathbb{R}},$

The projection of a given point $x$ on the line is a vector $z$ located on the line, that is closest to $x$ (in Euclidean norm). This corresponds to a simple optimization problem:

$\min\limits_{t} ||x-x_0-tu||_2.$

This particular problem is part of a general class of optimization problems known as least-squares. It is also a special case of a Euclidean projection on a general set.

Projection of the vector $x=(1.6, 2.28)$ on a line passing through the origin ( $x_0 = 0$ ) and with (normalized) direction $u = (0.8944, 0.4472)$ . At optimality the ‘‘residual’’ vector $x-z$ is orthogonal to the line, hence $z = tu$ , with $t = x^Tu = 2.0035$ . Any other point on the line is farther away from the point $x$ than its projection $z$ is.

The scalar $t = u^T x$ , ie the scalar product between $x$ and $u$ , is the component of $x$ along the normalized direction $u$ .

Closed-form expression

Assuming that $u$ is normalized, so that $||u||_2=1$ , the objective function of the projection problem reads, after squaring:

$||x-x_0-tu||_2^2 = t^2 - 2tu^T(x-x_0) + ||x-x_0||_2^2 = (t-u^T(x-x_0))^2 + constant.$

Thus, the optimal solution to the projection problem is

$t^* = u^T(x-x_0),$

and the expression for the projected vector is

$z^* = x_0 + t^*u = x_0 + u^T(x-x_0)u.$

The scalar product $u^T(x-x_0)$ is the component of $x-x_0$ along $u$ .

In the case when $u$ is not normalized, the expression is obtained by replacing $u$ with its scaled version $u/||u||_2$ :

$z^* = x_0 + t^*u = x_0 + \frac{u^T(x-x_0)}{u^T u}u.$

Interpreting the scalar product

We can now interpret the scalar product between two non-zero vectors $x, u$ , by applying the previous derivation to the projection of $x$ on the line of direction $u$ passing through the origin. If $u$ is normalized ( $||u||_2 = 1$ ), then the projection of $x$ on ${\bf L}$ is $z^* = (u^T x)u$ . Its length is $||z^*||_2 = |u^Tx|$ . (See above figure.)

In general, the scalar product $u^T x$ is simply the component of $x$ along the normalized direction $u/||u||_2$ defined by $u$ .

Projection on a line

Definition

Closed-form expression

Interpreting the scalar product

License

Share This Book