Orthogonalization: the Gram-Schmidt procedure
- Orthogonalization
- Projection on a line
- Gram-Schmidt procedure
A basis ![]() is said to be orthogonal if
is said to be orthogonal if ![]() if
if ![]() . If in addition,
. If in addition, ![]() , we say that the basis is orthonormal.
, we say that the basis is orthonormal.
Example: An orthonormal basis in ![]() . The collection of vectors
. The collection of vectors ![]() , with
, with
(1) 
(2) 
forms an orthonormal basis of ![]() .
.
What is orthogonalization?
Orthogonalization refers to a procedure that finds an orthonormal basis of the span of given vectors.
Given vectors ![]() , an orthogonalization procedure computes vectors
, an orthogonalization procedure computes vectors ![]() such that
such that
where r is the dimension of ![]() , and
, and
That is, the vectors ![]() form an orthonormal basis for the span of the vectors
form an orthonormal basis for the span of the vectors ![]() .
.
Basic step: projection on a line
A basic step in the procedure consists in projecting a vector on a line passing through zero. Consider the line
where ![]() is given, and normalized (
is given, and normalized (![]() ).
).
The projection of a given point ![]() on the line is a vector
on the line is a vector ![]() located on the line, that is closest to
located on the line, that is closest to  (in Euclidean norm). This corresponds to a simple optimization problem:
(in Euclidean norm). This corresponds to a simple optimization problem:
The vector ![]() , where
, where ![]() is the optimal value, is referred to as the projection of
is the optimal value, is referred to as the projection of ![]() on the line
on the line ![]() . As seen here, the solution of this simple problem has a closed-form expression:
. As seen here, the solution of this simple problem has a closed-form expression:
Note that the vector  can now be written as a sum of its projection and another vector that is orthogonal to the projection:
can now be written as a sum of its projection and another vector that is orthogonal to the projection:
where ![]() and
and ![]() are orthogonal. The vector
are orthogonal. The vector ![]() can be interpreted as the result of removing the component of
can be interpreted as the result of removing the component of ![]() along
along ![]() .
.
Gram-Schmidt procedure
The Gram-Schmidt procedure is a particular orthogonalization algorithm. The basic idea is to first orthogonalize each vector w.r.t. previous ones; then normalize result to have norm one.
Case when the vectors are independent
Let us assume that the vectors ![]() are linearly independent. The GS algorithm is as follows.
are linearly independent. The GS algorithm is as follows.
Gram-Schmidt procedure:
- set
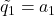 .
. - normalize: set
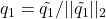 .
. - remove component of
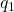 in
in 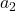 : set
: set 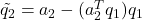 .
. - normalize: set
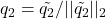 .
. - remove components of
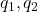 in
in  : set
: set 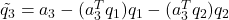 .
. - normalize: set
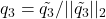 .
. - etc.
 |
The image of the left shows the GS procedure applied to the case of two vectors in two dimensions. We first set the first vector to be a normalized version of the first vector |
The GS process is well-defined, since at each step ![]() (otherwise this would contradict the linear independence of the
(otherwise this would contradict the linear independence of the ![]() ‘s).
‘s).
General case: the vectors may be dependent
It is possible to modify the algorithm to allow it to handle the case when the ![]() ‘s are not linearly independent. If at step
‘s are not linearly independent. If at step ![]() , we find
, we find ![]() , then we directly jump at the next step.
, then we directly jump at the next step.
Modified Gram-Schmidt procedure:
- set
 .
. - for
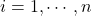 :
:
- set
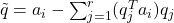 .
. - if
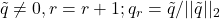 .
.
- set
On exit, the integer ![]() is the dimension of the span of the vectors
is the dimension of the span of the vectors ![]() .
.
