Ordinary Least-Squares Problem

L. El Ghaoui

Ordinary Least-Squares Problem

Definition
Interpretations
Solution via QR decomposition (full rank case)
Optimal solution (general case)

Definition

The Ordinary Least-Squares (OLS, or LS) problem is defined as

$\min _x\|A x-y\|_2^2$

where $A \in \mathbf{R}^{m \times n}, y \in \mathbf{R}^m$ are given. Together, the pair $(A, y)$ is referred to as the problem data. The vector $y$ is often referred to as the ‘‘measurement” or “output” vector, and the data matrix $A$ as the ‘‘design‘‘ or ‘‘input‘‘ matrix. The vector $r:=y-A x$ is referred to as the residual error vector.

Note that the problem is equivalent to one where the norm is not squared. Taking the squares is done for the convenience of the solution.

Interpretations

Interpretation as projection on the range

We can interpret the problem in terms of the columns of $A$ , as follows. Assume that $A=\left[a_1, \ldots, a_n\right]$ , where $a_j \in \mathbf{R}^m$ is the $j$ -th column of $A, j=1, \ldots, n$ . The problem reads

$\min _x\left\|\sum_{j=1}^n x_j a_j-y\right\|_2 .$

In this sense, we are trying to find the best approximation of $y$ in terms of a linear combination of the columns of $A$ . Thus, the OLS problem amounts to project (find the minimum Euclidean distance) the vector $y$ on the span of the vectors $a_j$ ‘s (that is to say: the range of $A$ ).

As seen in the picture, at optimum the residual vector $A x-y$ is orthogonal to the range of $A$ .

Examples:

Image compression via least-squares.

Interpretation as minimum distance to feasibility

The OLS problem is usually applied to problems where the linear $Ax=y$ is not feasible, that is, there is no solution to $Ax=y$ .

The OLS can be interpreted as finding the smallest (in Euclidean norm sense) perturbation of the right-hand side, $\delta y$ , such that the linear equation

$A x=y+\delta y$

becomes feasible. In this sense, the OLS formulation implicitly assumes that the data matrix $A$ of the problem is known exactly, while only the right-hand side is subject to perturbation, or measurement errors. A more elaborate model, total least-squares, takes into account errors in both $A$ and $y$ .

Interpretation as regression

We can also interpret the problem in terms of the rows of $A$ , as follows. Assume that $A^T=\left[a_1, \ldots, a_m\right]$ , where $a_i^T \in \mathbf{R}^m$ is the $i$ -th row of $A, i=1, \ldots, m$ . The problem reads

$\min _x \sum_{i=1}^m\left(y_i-a_i^T x\right)^2 .$

In this sense, we are trying to fit each component of $y$ as a linear combination of the corresponding input $a_i$ , with $x$ as the coefficients of this linear combination.

Examples:

Solution via QR decomposition (full rank case)

Assume that the matrix $A \in \mathbf{m} \times \mathbf{n}$ is tall ( $m \geq n$ ) and full column rank. Then the solution to the problem is unique and given by

$x^*=\left(A^T A\right)^{-1} A^T y .$

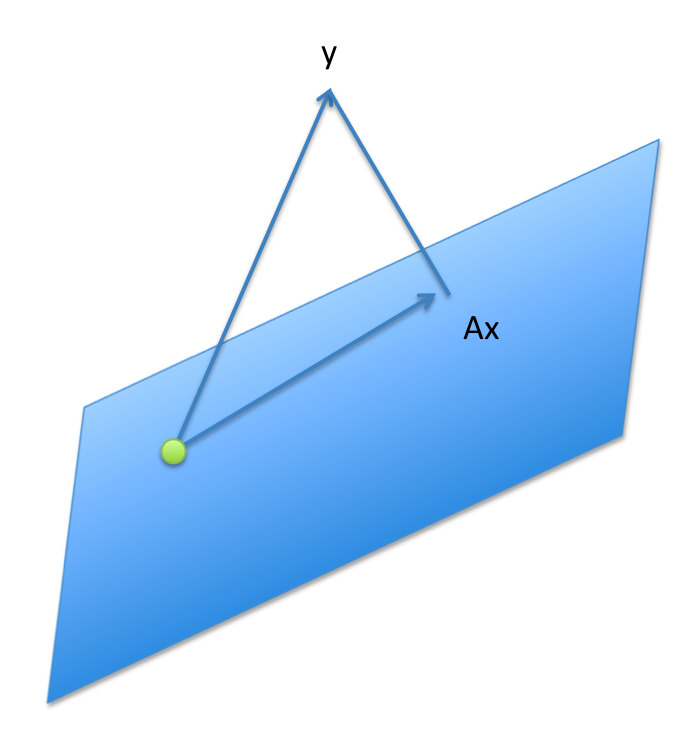
This can be seen by simply taking the gradient (vector of derivatives) of the objective function, which leads to the optimality condition $A^T(A x-y)=0$ . Geometrically, the residual vector $A x-y$ is orthogonal to the span of the columns of $A$ , as seen in the picture above.

We can also prove this via the QR decomposition of the matrix $A: A=Q R$ with $Q$ a $m \times n$ matrix with orthonormal columns ( $Q^T Q=I_n$ ) and $R$ a $n \times n$ upper-triangular, invertible matrix. Noting that
$\|A x-y\|_2^2=x^T A^T A x-2 x^T A^T y+y^T y=x^T R^T R x-2 x^T R^T Q^T y+y^T y=\left\|R x-Q^T y\right\|_2^2+y^T\left(I-Q Q^T\right) y$

and exploiting the fact that $R$ is invertible, we obtain the optimal solution $x^*=R^{-1} Q^T y$ . This is the same as the formula above, since

$\left(A^T A\right)^{-1} A^T y=\left(R^T Q^T Q R\right)^{-1} R^T Q^T y=\left(R^T R\right)^{-1} R^T Q^T y=R^{-1} Q^T y .$

Thus, to find the solution based on the QR decomposition, we just need to implement two steps:

Rotate the output vector: set $\bar{y}=Q^T y$ .
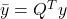Solve the triangular system 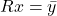$R x=\bar{y}$ by backwards substitution.

In Matlab, the backslash operator finds the (unique) solution when $A$ is full column rank.

Matlab syntax

>> x = A\y;

Optimal solution and optimal set

Recall that the optimal set of a minimization problem is its set of minimizers. For least-squares problems, the optimal set is an affine set, which reduces to a singleton when $A$ is full column rank.

In the general case ( $A$ is not necessarily tall, and /or not full rank) then the solution may not be unique. If $x^0$ is a particular solution, then $x=x^0+z$ is also a solution, if $z$ is such that $A z=0$ , that is, $z \in \mathbf{N}(A)$ . That is, the nullspace of $A$ describes the ambiguity of solutions. In mathematical terms: