Nomenclature of a toy 2D optimization problem

L. El Ghaoui

Nomenclature of a toy 2D optimization problem

Consider the toy optimization problem in two variables:

$\min _x x_1^2-x_1 x_2+2x_2^2-3x_1-1.5x_2: -1 \leq x_1 \leq 2, \quad 0 \leq x_2 \leq 3 .$

For this problem:

The optimal value is $p^*=-10.2667$ .
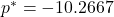The optimal set is the singleton 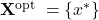$\mathbf{X}^{\text {opt }}=\left\{x^*\right\}$ , with

$x^*=\left(\begin{array}{c} 2.00 \\ 1.33 \end{array}\right) .$

Since the optimal set is not empty, the problem is attained.

An $\epsilon$ -sub-optimal set for the toy problem above is shown (in a darker color), for $\epsilon=0.9$ . This corresponds to the set of feasible points that achieves an objective value less or equal to $p^*+\epsilon$ .

See also:

Geometric view of the toy problem.

Nomenclature of a toy 2D optimization problem

License

Share This Book