Linear and Quadratic Programming

A linear program (LP) is an optimization problem in standard form, in which all the functions involved are affine. The feasible set is thus a polyhedron, that is, an intersection of half-spaces. Polyhedral functions are functions with a polyhedral epigraph and include maxima or sums of maxima of linear or affine functions. Such functions can be minimized via LP.

Quadratic programs (QPs) offer an extension of linear programs, in which all the constraint functions involved are affine, and the objective is the sum of a linear function and a positive semi-definite quadratic form. QPs generalize both LPs and ordinary least-squares: the objective function is the same as in ordinary least-squares, and the problem includes polyhedral constraints, just as in LP.

Outline

• Polyhedra
• Standard forms of linear and quadratic programs
• Polyhedral functions and their minimization
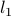• Cardinality minimization and the -norm trick
• Applications
• Exercises