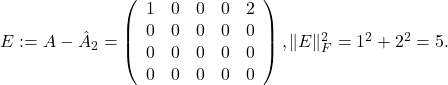Low-rank approximation of a 4 x 5 matrix via its SVD
Returning to this example, involving a matrix with row size ![]() and column size
and column size ![]() :
:

As seen here, the SVD is given by ![]() , with
, with
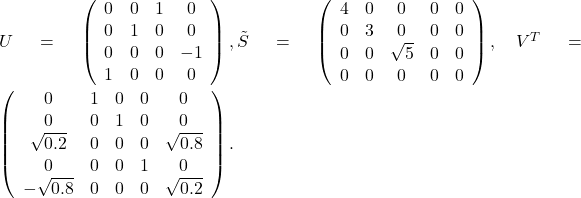
The matrix is rank ![]() . A rank-two approximation is given by zeroing out the smallest singular value, which produces
. A rank-two approximation is given by zeroing out the smallest singular value, which produces

We check that the Frobenius norm of the error ![]() is the sum of singular values we have zeroed out, which here reduces to
is the sum of singular values we have zeroed out, which here reduces to ![]() :
: