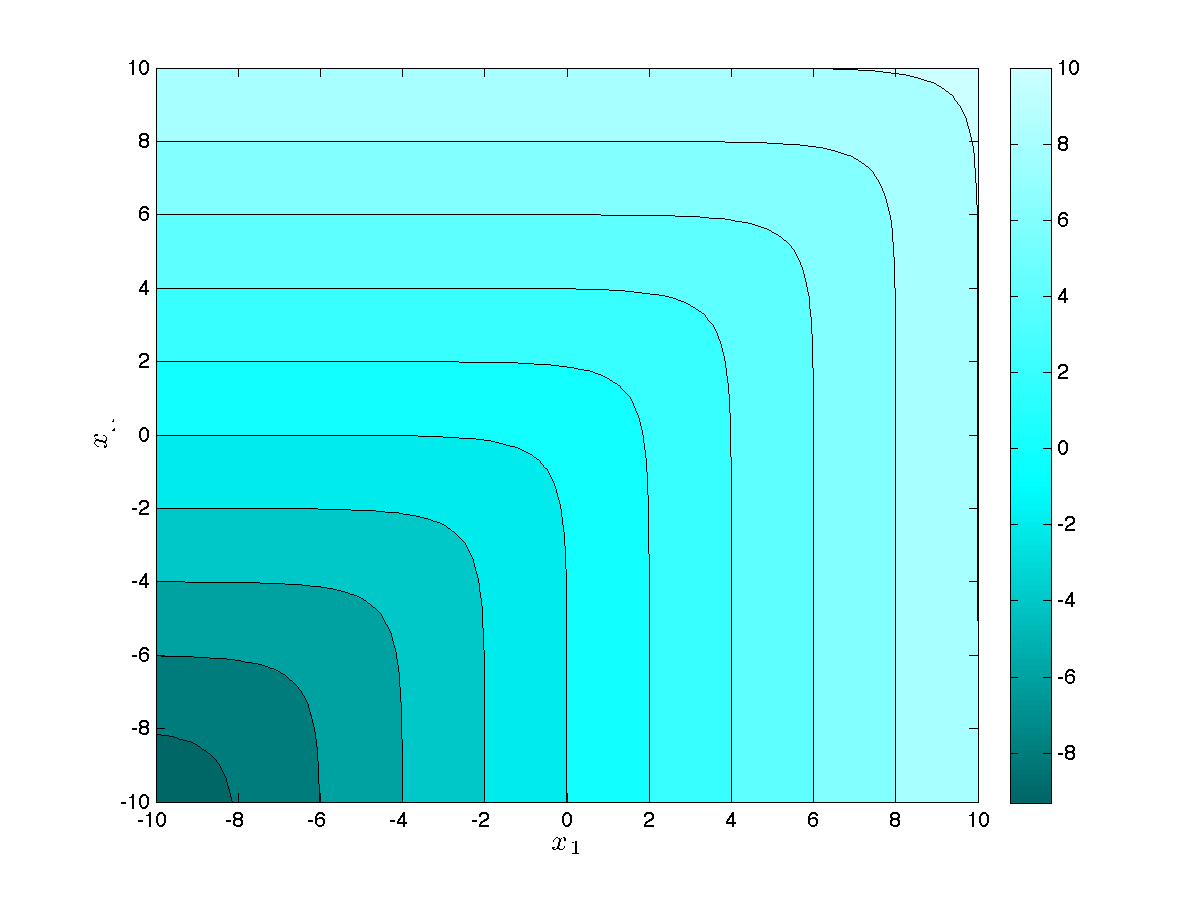
Log-Sum-Exp (LSE) Function and Properties

L. El Ghaoui

Log-Sum-Exp (LSE) Function and Properties

The log-sum-exp (LSE) function in $\mathbb{R}^n$ is the function $f: \mathbb{R}^n \rightarrow \mathbb{R}$ , with domain the whole space $\mathbb{R}^n$ , and value at a point $x \in \mathbb{R}^n$ given by

$f(x) = \log\left(\sum\limits_{i=1}^{n} e^{x_i}\right)$

The log-sum-exp function in $\mathbb{R}^2$ . For large positive values, the function is a smooth approximation to the maximum function $(x_1,x_2) \rightarrow \max(x_1, x_2)$

The log-sum-exp function is increasing with respect to each argument, and convex.

Proof: The monotonicity of the log-sum-exp function is obvious. The convexity is obtained as follows. As seen here, the Hessian of the log-sum-exp function is

$\nabla^2 f(x) = \frac{1}{S(x)^2} (S(x){\bf diag}(s(x)) - s(x)s(x)^T),$

where $s(x) = (e^{x_1}, e^{x_2},\cdots, e^{x_n})$ , and $S(x) = \sum\limits_{i=1}^{n} s_i(x)$

We need to check that for every $z \in \mathbb{R}^n$ , we have $z^T\nabla^2 f(x)z \geq 0$ . Let us fix a vector $z \in \mathbb{R}^n$ . We have

$\begin{aligned} S(x)^2 \cdot z^T \nabla^2 f(x) z & =z^T\left(S(x) {\bf diag}(s(x))-s(x) s(x)^T\right) z \\ & =\left(\sum_{i=1}^n s_i(x) z_i^2\right)\left(\sum_{i=1}^n s_i(x)\right)-\left(\sum_{i=1}^n s_i(x) z_i\right)^2 \geq 0 \end{aligned}$

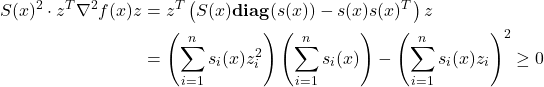
due to the Cauchy-Schwartz inequality.

Log-Sum-Exp (LSE) Function and Properties

License

Share This Book