Lines in high dimension

L. El Ghaoui

Lines in high dimension

The line in $\mathbb{R}^n$ passing through $x_0 \in \mathbb{R}^n$ and with direction $u \in \mathbb{R}^n$ , $u \neq 0$ , is the set of vectors $x$ such that $x-x_0$ is parallel to $u$ :

$\{x_0 + tu| t \in \mathbb{R}\}.$

We can always assume without loss of generality that the direction $u$ is normalized, that is $||u||_2 = 1$ .

Lines are affine sets of dimension one (since they are translations of the span of one vector).

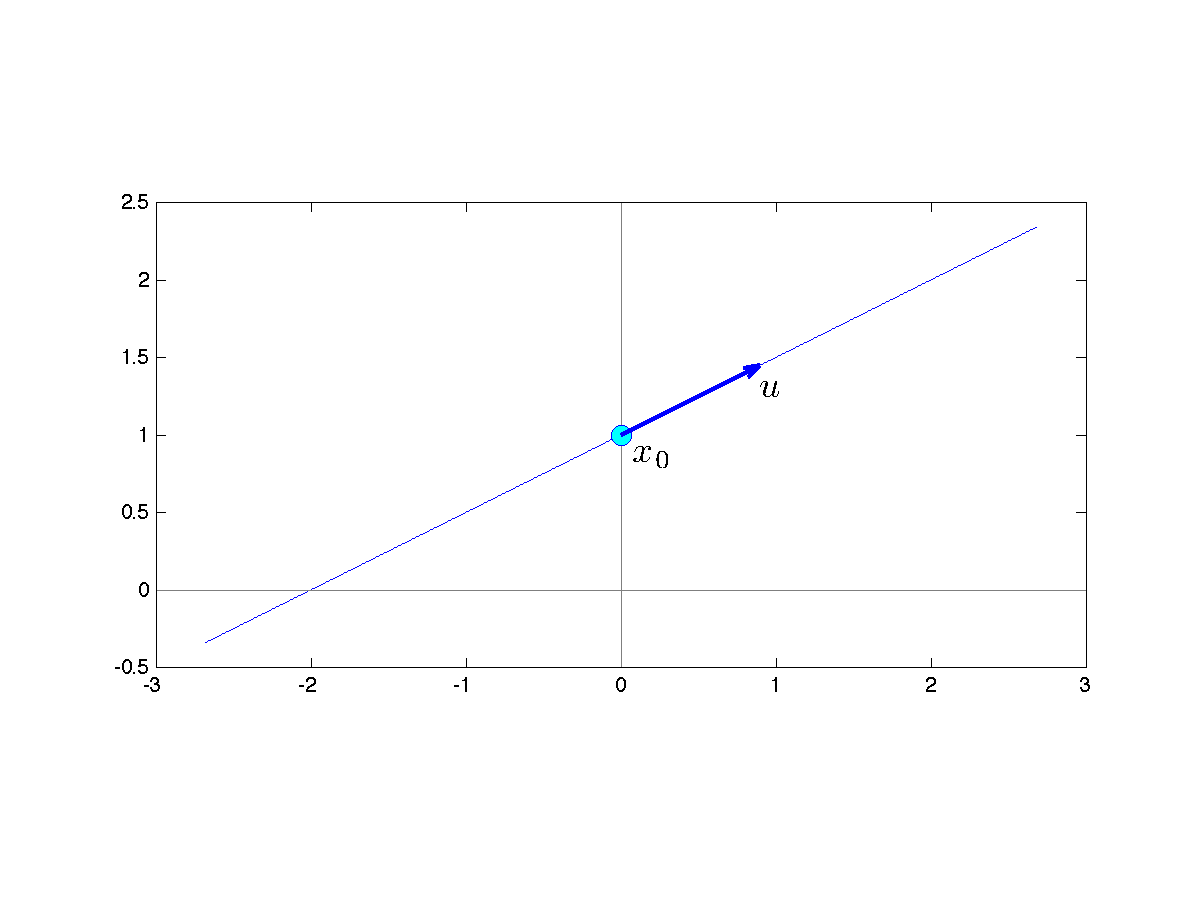A line in $\mathbb{R}^2$ passing through the point $x_0 = (2,0)$ , with (normalized) direction $u=(0.8944, 0.4472)$ .

Lines in high dimension

License

Share This Book