Linearly Constrained Least-Squares Problems

L. El Ghaoui

Linearly Constrained Least-Squares Problems

Linearly-constrained least-squares
Minimum-norm solutions to linear equations

Linearly constrained least-squares

Definition

An interesting variant of the ordinary least-squares problem involves equality constraints on the decision variable :

$\min\limits_x ||Ax-y||_2^2:Cx=d,$

where $C \in R^{p \times n}$ , and $d \in R^p$ are given.

Examples:

Minimum-variance portfolio.

Solution

We can express the solution by first computing the nullspace of $C$ . Assuming that the feasible set of the constrained LS problem is not empty, it can be expressed as

$X={x_0+Nz : z \in R^k},$

where 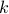is the dimension of the nullspace of $C$ , and $x_0$ is a particular solution to the equation $Cx=d$ .

Expressing in terms of the free variable $z$ , we can write the constrained problem as an unconstrained one:

$\min\limits_{x} ||\tilde{A}z-\tilde{y}||_2$

where $\tilde{A}:=AN$ , and $\tilde{y}=y-Ax_0$ .

Minimum-norm solution to linear equations

A special case of linearly constrained LS is

$\min\limits_x ||x||_2 : Ax = y,$

in which we implicitly assume that the linear equation in $x$ : $Ax=y$ , has a solution, that is, $y$ is in the range of $A$ .

The above problem allows selecting a particular solution to a linear equation, in the case when there are possibly many, that is, the linear system $aX=Y$ is under-determined.

As seen here, when $A$ is full row rank, the matrix $AA^T$ is invertible, and the above has the closed-form solution

$x^*=A^T(AA^T)^{-1}y.$

Examples: Control positioning of a mass.

Linearly Constrained Least-Squares Problems

Linearly constrained least-squares

Definition

Solution

Minimum-norm solution to linear equations

License

Share This Book