Linearization of a non-linear function
The log-sum-exp function
admits the gradient at the point ![]() given by
given by
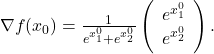
Hence ![]() can be approximated near
can be approximated near ![]() by the linear function
by the linear function
The log-sum-exp function
admits the gradient at the point ![]() given by
given by
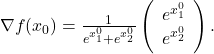
Hence ![]() can be approximated near
can be approximated near ![]() by the linear function
by the linear function