Least-squares and SVD

L. El Ghaoui

Least-squares and SVD

Set of solutions via the pseudo inverse
Sensitivity analysis
BLUE property

Set of solutions

The following theorem provides all the solutions (optimal set) of a least-squares problem.

Theorem: optimal set of ordinary least-squares

The optimal set of the OLS problem

$p^*:=\min _x\|A x-y\|_2$

can be expressed as

$\mathbf{X}^{\text {opt }}=A^{\dagger} y+\mathbf{N}(A) .$

where $A^{\dagger}$ is the pseudo-inverse of $A$ , and $A^{\dagger} y$ is the minimum-norm point in the optimal set. If $A$ is full column rank, the solution is unique, and equal to

$x^*=A^{\dagger} y=\left(A^T A\right)^{-1} A^T y .$

In general, the particular solution $A^{\dagger} y$ is the minimum-norm solution to the least-squares problem.

Proof: here.

Sensitivity analysis

We consider the situation where

$y+\delta y=A x,$

with

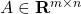$A \in \mathbf{R}^{m \times n}$ the data matrix (known), with $A$ full column rank (hence $m \geq n$ ).
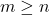$y \in \mathbf{R}^m$ is the measurement (known).
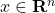$x \in \mathbf{R}^n$ is the vector to be estimated (unknown).
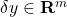$\delta y \in \mathbf{R}^m$ is a measurement noise or error (unknown).

We can use OLS to provide an estimate $\hat{x}_{\text {OLS }}$ of $X$ . The idea is to seek the smallest vector $\delta y$ such that the above equation becomes feasible, that is,

$\min _{x, \delta y}\|\delta y\|_2: y+\delta y=A x .$

This leads to the OLS problem:

$\min _x\|A x-y\|_2 .$

Since $A$ is full column rank, its SVD can be expressed as

$A=U\left(\begin{array}{c} \Sigma \\ 0 \end{array}\right) V^T,$

where $\Sigma=\operatorname{diag}\left(\sigma_1, \ldots, \sigma_m\right)$ contains the singular values of $A$ , with $\sigma_1 \geq \ldots \geq \sigma_m>0$ .

Since $A$ is full column rank, the solution $\hat{x}_{\mathrm{LS}}$ to the OLS problem is unique, and can be written as a linear function of the measurement vector $y$ :

$\hat{x}_{\mathrm{LS}}=A^{\dagger} y,$

with $A^{\dagger}$ the pseudo-inverse of $A$ . Again, since $A$ is full column rank,

$A^{\dagger}=\left(A^T A\right)^{-1} A^T=V\left(\begin{array}{cc} \Sigma^{-1} & 0 \end{array}\right) U^T .$

The OLS formulation provides an estimate $\hat{x}$ of the input $x$ such that the residual error vector $Ax-y$ is minimized in norm. We are interested in analyzing the impact of perturbations in the vector $y$ , on the resulting solution $\hat{x}_{LS}$ . We begin by analyzing the absolute errors in the estimate and then turn to the analysis of relative errors.

Set of possible errors

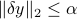
Let us assume a simple model of potential perturbations: we assume that $\delta y$ belongs to a unit ball: |delta y |_2 le alpha $||\delta y||_2 \leq \alpha$ , where $\alpha>0$ is given. We will assume $\alpha=1$ for simplicity; the analysis is easily extended to any $\alpha>0$ .

We have

$\begin{aligned} \delta x:=x-\hat{x} & =x-A^{\dagger} y \\ & =x-A^{\dagger}(A x-\delta y) \\ & =\left(I-A^{\dagger} A\right) x+A^{\dagger} \delta y \\ & =A^{\dagger} \delta y . \end{aligned}$

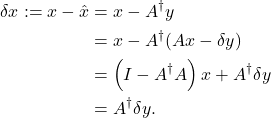
In the above, we have exploited the fact that $A^{\dagger}$ is a left inverse of $A$ , that is, $A^{\dagger} A=I_n$ .

The set of possible errors on the solution $\delta x$ is then given by

$\mathbf{E}=\left\{A^{\dagger} \delta y:\|\delta y\|_2 \leq 1\right\},$

which is an ellipsoid centered at zero, with principal axes given by the singular values of $A^{\dagger}$ . This ellipsoid can be interpreted as an ellipsoid of confidence for the estimate $\hat{x}$ , with size and shape determined by the matrix $A^{\dagger}(A^{\dagger})^T$ .

We can draw several conclusions from this analysis:

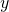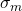The largest absolute error in the solution that can result from a unit-norm, additive perturbation on $y$ is of the order of $1 / \sigma_m$ , where $\sigma_m$ is the smallest singular value of $A$ .
The largest relative error is 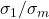$\sigma_1 / \sigma_m$ , the condition number of $A$ .

BLUE property

We now return to the case of an OLS with full column rank matrix $A$ .

Unbiased linear estimators

Consider the family of linear estimators, which are of the form

$\hat{x}=B y,$

where $B \in \mathbf{R}^{n \times m}$ . To this estimator, we associate the error

$\delta x=x-\hat{x}=x-B y=x-B(A x-\delta y)=(I-B A) x+B \delta y .$

We say that the estimator (as determined by matrix $B$ ) is unbiased if the first term is zero:

$B A=I .$

Unbiased estimators only exist when the above equation is feasible, that is, $A$ has a left inverse. This is equivalent to our condition that $A$ be full column rank. Since $A^{\dagger}$ is a left-inverse of $A$ , the OLS estimator is a particular case of an unbiased linear estimator.

Best unbiased linear estimator

The above analysis leads to the following question: which is the best unbiased linear estimator? One way to formulate this problem is to assume that the perturbation vector $\delta y$ is bounded in some way, and try to minimize the possible impact of such bounded errors on the solution.

Let us assume that $\delta y$ belongs to a unit ball: $\|\delta y\|_2 \leq 1$ . The set of resulting errors on the solution $\delta x$ is then

$\mathbf{E}=\left\{B \delta y:\|\delta\|_2 \leq 1\right\},$

which is an ellipsoid centered at zero, with principal axes given by the singular values of $B$ . This ellipsoid can be interpreted as an ellipsoid of confidence for the estimate $\hat{x}$ , with size and shape determined by the matrix $BB^T$ .

It can be shown that the OLS estimator is optimal in the sense that it provides the ‘‘smallest’’ ellipsoid of confidence among all unbiased linear estimators. Specifically:

$B B^T \succeq A^{\dagger}\left(A^{\dagger}\right)^T$

This optimality of the LS estimator is referred to as the BLUE (Best Linear Unbiased Estimator) property.

Least-squares and SVD

Set of solutions

Sensitivity analysis

Set of possible errors

BLUE property

Unbiased linear estimators

Best unbiased linear estimator

License

Share This Book