Laplacian matrix of a graph

Another important symmetric matrix associated with a graph is the Laplacian matrix. This is the matrix , with as the arc-node incidence matrix. It can be shown that the element of the Laplacian matrix is given by

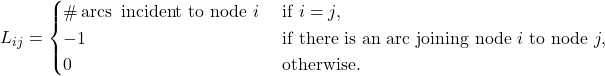
See also:

• Arc-node incidence matrix of a graph.
• Edge-weight matrix of a graph.