Kernel Least-Squares

L. El Ghaoui

Kernel Least-Squares

Motivations
The kernel trick
Nonlinear case
Examples of kernels
Kernels in practice

Motivations

Consider a linear auto-regressive model for time-series, where $y_t$ is a linear function of $y_{t-1},y_{t-2}$

$y_t=w_1+w_2 y_{t-1}+w_3 y_{t-2}, \quad t=1, \ldots, T$

This writes $y_t=w^T x_t$ , with $x_t$ the “feature vectors”

$x_t:=\left(1, y_{t-1}, y_{t-2}\right), t=1, \ldots, T .$

We can fit this model based on historical data via least-squares:

$\min _{\infty}\left\|X^T w-y\right\|_2^2$

The associated prediction rule is $\hat{y}_{T+1}=w_1+w_2 y_T+w_3 y_{T-1}=w^T x_{T+1}$ .
We can introduce a non-linear version, where $y_t$ is a quadratic function of $y_{t-1}, y_{t-2}$

$y_t=w_1+w_2 y_{t-1}+w_3 y_{t-2}+w_4 y_{t-1}^2+w_5 y_{t-1} y_{t-2}+w_6 y_{t-2}^2 .$

This writes $y_t=w^T \phi\left(x_t\right)$ , with $\phi\left(x_t\right)$ the augmented feature vectors

$\phi\left(x_t\right):=\left(1, y_{t-1}, y_{t-2}, y_{t-1}^2, y_{t-1} y_{t-2}, y_{t-2}^2\right) .$

Everything is the same as before, with $x$ replaced by $\phi(x)$ .
It appears that the size of the least-squares problem grows quickly with the degree of the feature vectors. How do we do it in a computationally efficient manner?

The kernel trick

We exploit a simple fact: in the least-squares problem

$\min _w\left\|X^T w-y\right\|_2^2+\lambda\|w\|_2^2$

the optimal $w$ lies in the span of the data points $\left(x_1, \ldots, x_m\right)$ :

$w=X v$

for some vector $v \in \mathbf{R}^m$ . Indeed, from the fundamental theorem of linear algebra, every $w \in \mathbf{R}^n$ can be written as the sum of two orthogonal vectors:

$w=X v+r$

where $X^T r=0$ (that is, $r$ is in the nullspace $N\left(X^T\right)$ ).
Hence the least-squares problem depends only on $K:=X^T X$ :

$\min _v\|K v-y\|_2^2+\lambda v^T K v .$

The prediction rule depends on the scalar products between new point $x$ and the data points $x_1, \ldots, x_m$ :

$w^T x=v^T X^T x=v^T k, \quad k:=X^T x=\left(x^T x_1, \ldots, x^T x_m\right) .$

Once $K$ is formed (this takes $O(n)$ ), then the training problem has only $m$ variables. When $n>>$ , this leads to a dramatic reduction in problem size.

Nonlinear case

In the nonlinear case, we simply replace the feature vectors $x_{\text {; }}$ with some “augmented” feature vectors $\phi\left(x_i\right)$ , with $\phi$ a non-linear mapping.
This leads to the modified kernel matrix

$K_{i j}=\phi\left(x_i\right)^T \phi\left(x_j\right), \quad 1 \leq i, j \leq m .$

The kernel function associated with mapping $\phi$ is

$k(x, z)=\phi(x)^T \phi(z) .$

It provides information about the metric in the feature space, eg:

$\|\phi(x)-\phi(z)\|_2^2=k(x, x)-2 k(x, z)+k(z, z) .$

The computational effort involved in

solving the training problem;
making a prediction,

depends only on our ability to quickly evaluate such scalar products. We can’t choose $k$ arbitrarily; it has to satisfy the above for some $\phi$ .

Examples of kernels

A variety of kernels are available. Some are adapted to the structure of data, for example, text or images. Here are a few popular choices.

Polynomial kernels

Regression with quadratic functions involves feature vectors

$\phi(x)=\left(1, x_1, x_2, x_1^2, x_1 x_2, x_2^2\right) .$

In fact, given two vectors $x, z \in \mathbf{R}^2$ , we have

$\phi(x)^T \phi(z)=\left(1+x^T z\right)^2 .$

More generally when $\phi(x)$ is the vector formed with all the products between the components of $x \in \mathbf{R}^n$ , up to degree $d$ , then for any two vectors $x, z \in \mathbf{R}^n$ ,

$\phi(x)^T \phi(z)=\left(1+x^T z\right)^d .$

The computational effort grows linearly in $n$ .

This represents a dramatic reduction in speed over the ‘‘brute force’’ approach:

Form $\phi(x), \phi(z)$ ;
evaluate 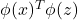$\phi(x)^T \phi(z)$ . In the above approach, the computational effort grows as $n^d$ .

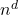Gaussian kernels

Gaussian kernel function:

$k(x, z)=\exp \left(-\frac{\|x-z\|_2^2}{2 \sigma^2}\right),$

where $\sigma>0$ is a scale parameter This allows ignoring points that are too far apart. Corresponds to a non-linear mapping $\phi$ to infinite-dimensional feature space.

Other kernels

There is a large variety (a zoo?) of other kernels, some adapted to the structure of data (text, images, etc).

Kernels in practice

Kernels need to be chosen by the user.
The choice is not always obvious; Gaussian or polynomial kernels are popular.
We control over-fitting via cross-validation (to choose, say, the scale parameter of Gaussian kernel, or degree of the polynomial kernel).

Kernel Least-Squares

Motivations

The kernel trick

Nonlinear case

Examples of kernels

Polynomial kernels

Gaussian kernels

Other kernels

Kernels in practice

License

Share This Book