12 Index
A
- Absorbtion spectrometry
- Affine function
- Affine set
- Angle between vectors
- Auto-regressive models for time-series prediction
B
- Backward substitution method for solving triangular systems of linear equations
- Bag-of-word representation of text
- Basis of a subspace
- Beer-Lambert law
C
- CAT scan imaging
- Cauchy-Schwartz inequality
- Cardinality of a vector
- Cardinality minimization, see also l_1-norm
- Circuit design via Geometric Programming
- Combinational logic in circuit design
- Componentwise inequality between vectors
- Condition number of a matrix
- Convex function
- Convex optimization problem
- Covariance matrix
- CVX
D
- Determinant of a square matrix
- Dimension of an affine set
- Domain of a function
- Duality: weak, strong
- Dual norm
- Dual problem
- Dual function
- Dual norm, see also norm
- Dyad
E
- Eigenvalue decomposition (EVD) of a square, symmetric matrix
- Epigraph of a function
- Expected value of a random variable
F
- Feasible point, feasible set
- First-order approximation
- Frobenius norm of a matrix
- Function
- Fundamental theorem of linear algebra
G
- Geometric program (GP)
- Global optimum
- Gradient of a function
- Gradient methods, for solving convex programs
- Gram matrix
- Gram-Schmidt (GS) procedure
- Graph of a function
H
I
- Image compression
- Incidence matrix of a graph
- Independent set of vectors
- Interior-point methods, for solving convex programs
- Inverse of a matrix
J
- Jacobian matrix of a non-linear map
K
- Kernel matrix, kernel trick
L
- Laplacian of a graph
- Lagragian of an optimization problem
- Laplace formula for the determinant of a matrix
- Largest singular value (LSV) norm of a matrix
- Least-squares
- Leibnitz formula for the determinant of a matrix
- Left inverse of a matrix
- Linear function
- Linear matrix inequality
- Linear program (LP)
- Linear regression
- Local optimum
- Log-return of a financial asset
- Log-sum-exp function
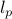 norms of a vector:
norms of a vector: 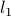 norm,
norm, 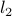 -norm (also called Euclidean norm),
-norm (also called Euclidean norm), 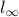 norm.
norm.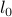 norm, or cardinality, of a vector.
norm, or cardinality, of a vector.
M
N
- Norms: general definition, for vectors, for matrices; see also dual norm
- Nullspace of a matrix
O
- Optimal point, optimal value, optimal set
- Orthogonal: vectors, matrices
P
- Permutation matrix
- Point-wise maximum of functions
- Polyhedron
- Polyhedral function
- Positive-definite
- Power laws
- Principal Component Analysis (PCA)
- Probability simplex
- Projection: on a line
- Pseudo-inverse of a matrix
Q
R
- Range of a matrix
- Rank of a matrix
- Rate of return of a financial asset
- Rayleigh quotient
- Regression: Linear
- Right inverse of a matrix
- Robust linear program
S
- Sample mean, sample standard deviation, sample covariance matrix
- Scalar product: for vectors, for matrices
- Second-order approximation of a function
- Second-order cone
- Second-order cone program (SOCP)
- Semidefinite program (SDP)
- Singular value of a general matrix
- Singular value decomposition (SVD)
- Slater’s condition for strong duality
- Spectral theorem, or symmetric eigenvalue decomposition (SED) theorem
- Symmetric matrix
T
- Tomography
- Trace of a matrix
- Triangle inequality
- Triangular matrices
- Triangular systems of linear equations, see also backward substitution algorithm
U
- Unconstrained optimization
- Unitary matrix (see also Orthogonal matrix)
