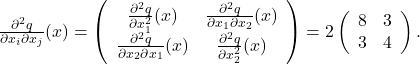Hessian of a quadratic function
For quadratic functions, the Hessian (matrix of second-derivatives) is a constant matrix, that is, it does not depend on the variable ![]() .
.
As a specific example, consider the quadratic function
The Hessian is given by
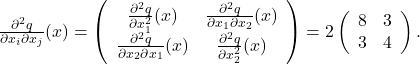
For quadratic functions, the Hessian (matrix of second-derivatives) is a constant matrix, that is, it does not depend on the variable ![]() .
.
As a specific example, consider the quadratic function
The Hessian is given by