Gradient of a linear function
Consider the function ![]() , with values
, with values
Its gradient is constant, with values

For a given ![]() , the
, the 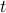 -level set is the set of points such that
-level set is the set of points such that ![]() :
:
The level sets are hyperplanes and are orthogonal to the gradient.
Consider the function ![]() , with values
, with values
Its gradient is constant, with values

For a given ![]() , the
, the 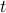 -level set is the set of points such that
-level set is the set of points such that ![]() :
:
The level sets are hyperplanes and are orthogonal to the gradient.