Exercises
Standard forms
- Regularization for noisy data. Consider a least-squares problem
in which the data matrix ![]() is noisy. Our specific noise model assumes that each row
is noisy. Our specific noise model assumes that each row ![]() has the form
has the form ![]() , where the noise vector
, where the noise vector ![]() has zero mean and covariance matrix
has zero mean and covariance matrix ![]() , with
, with ![]() a measure of the size of the noise. Therefore, now the matrix
a measure of the size of the noise. Therefore, now the matrix ![]() is a function of the uncertain vector
is a function of the uncertain vector ![]() , which we denote by
, which we denote by ![]() . We will write
. We will write ![]() to denote the matrix with rows
to denote the matrix with rows ![]() . We replace the original problem with
. We replace the original problem with
where ![]() denotes the expected value with respect to the random variable
denotes the expected value with respect to the random variable ![]() . Show that this problem can be written as
. Show that this problem can be written as
![]()
where ![]() is some regularization parameter, which you will determine. That is, regularized least-squares can be interpreted as a way to take into account uncertainties in the matrix
is some regularization parameter, which you will determine. That is, regularized least-squares can be interpreted as a way to take into account uncertainties in the matrix ![]() , in the expected value sense. Hint: compute the expected value of
, in the expected value sense. Hint: compute the expected value of ![]() , for a specific row index
, for a specific row index ![]() .
.
Applications
- Moore’s law describes a long-term trend in the history of computing hardware and states that the number of transistors that can be placed inexpensively on an integrated circuit has doubled approximately every two years. In this problem, we investigate the validity of the claim via least-squares.
- Using the problem data, show how to estimate the parameters
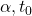 using least-squares, that is, via a problem of the form
using least-squares, that is, via a problem of the form
- Using the problem data, show how to estimate the parameters
Make sure to define precisely the data ![]() and how the variable
and how the variable ![]() relates to the original problem parameters
relates to the original problem parameters ![]() . (Use the notations
. (Use the notations ![]() for the number of processors, and
for the number of processors, and ![]() for the corresponding years. You can assume that no component of
for the corresponding years. You can assume that no component of ![]() is zero at optimum.)
is zero at optimum.)
-
- Is the solution to the problem above unique? Justify carefully your answer, and give the expression for the unique solution
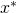 in terms of
in terms of 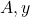 .
. - The solution to the problem yields
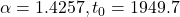 . Is this estimate consistent with the so-called Moore’s law, which states that the number of transistors per integrated circuit roughly doubles every two years?
. Is this estimate consistent with the so-called Moore’s law, which states that the number of transistors per integrated circuit roughly doubles every two years?
- Is the solution to the problem above unique? Justify carefully your answer, and give the expression for the unique solution
- The Michaelis–Menten model for enzyme kinetics relates the rate
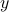 of an enzymatic reaction, to the concentration
of an enzymatic reaction, to the concentration  of a substrate, as follows:
of a substrate, as follows:
where ![]() , are parameters.
, are parameters.
-
- Show that the model can be expressed as a linear relation between the values
 and
and 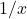 .
. - Use this expression to fit the parameter
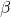 using linear least-squares.
using linear least-squares. - The above approach has been found to be quite sensitive to errors in input data. Can you experimentally confirm this opinion? Hint: generate noisy data from parameter values
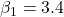 and
and 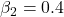 .
.
- Show that the model can be expressed as a linear relation between the values

