Exercises
SVD of simple matrices
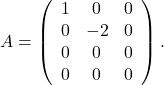
- Consider the matrix
-
- Find the range, nullspace, and rank of
 .
. - Find an SVD of
 .
. - Determine the set of solutions to the linear equation
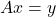 , with
, with
- Find the range, nullspace, and rank of
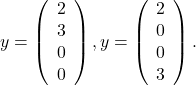
- Consider the
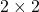 matrix
matrix
-
- What is an SVD of
 ? Express it as
? Express it as 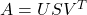 , with
, with 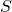 the diagonal matrix of singular values ordered in decreasing fashion. Make sure to check all the properties required for
the diagonal matrix of singular values ordered in decreasing fashion. Make sure to check all the properties required for 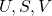 .
. - Find the semi-axis lengths and principal axes (minimum and maximum distance and associated directions from
 to the center) of the ellipsoid
to the center) of the ellipsoid
- What is an SVD of
Hint: Use the SVD of ![]() to show that every element of
to show that every element of ![]() is of the form
is of the form ![]() for some element
for some element ![]() in
in ![]() . That is,
. That is, ![]() . (In other words, the matrix
. (In other words, the matrix ![]() maps
maps ![]() into the set
into the set ![]() .) Then analyze the geometry of the simpler set
.) Then analyze the geometry of the simpler set ![]() .
.
-
- What is the set
 when we append a zero vector after the last column of
when we append a zero vector after the last column of  , that is
, that is  is replaced with
is replaced with 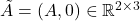 ?
? - The same question when we append a row after the last row of
 , that is,
, that is,  is replaced with
is replaced with ![Rendered by QuickLaTeX.com \tilde{A} = [A^T, 0]^T \in \mathbb{R}^{3 \times 2}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cd2f1f83adff52be42d88717f2655d52_l3.png) . Interpret geometrically your result.
. Interpret geometrically your result.
- What is the set
Rank and SVD
The image on the left shows a
|
Procrustes problem
The Orthogonal Procrustes problem is a problem of the form
where ![]() denotes the Frobenius norm, and the matrices
denotes the Frobenius norm, and the matrices ![]() ,
, ![]() are given. Here, the matrix variable
are given. Here, the matrix variable ![]() is constrained to have orthonormal columns. When
is constrained to have orthonormal columns. When ![]() , the problem can be interpreted geometrically as seeking a transformation of points (contained in
, the problem can be interpreted geometrically as seeking a transformation of points (contained in ![]() ) to other points (contained in
) to other points (contained in ![]() ) that involves only rotation.
) that involves only rotation.
- Show that the solution to the Procrustes problem above can be found via the SVD of the matrix
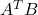 .
. - Derive a formula for the answer to the constrained least-squares problem
with ![]() ,
, ![]() given.
given.
SVD and projections
- We consider a set of
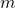 data points
data points  ,
, 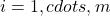 . We seek to find a line in
. We seek to find a line in 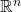 such that the sum of the squares of the distances from the points to the line is minimized. To simplify, we assume that the line goes through the origin.
such that the sum of the squares of the distances from the points to the line is minimized. To simplify, we assume that the line goes through the origin.
- Consider a line that goes through the origin
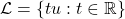 , where
, where 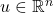 is given. (You can assume without loss of generality that
is given. (You can assume without loss of generality that 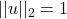 .) Find an expression for the projection of a given point
.) Find an expression for the projection of a given point  on
on  .
. - Now consider the
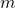 points and find an expression for the sum of the squares of the distances from the points to the line
points and find an expression for the sum of the squares of the distances from the points to the line  .
. - Explain how you would find the line via the SVD of the
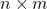 matrix
matrix ![Rendered by QuickLaTeX.com X = [x_1, \cdots, x_m]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-30eccf8a932d8a5cf1e610d516460b3c_l3.png) .
. - How would you address the problem without the restriction that the line has to pass through the origin?
- Consider a line that goes through the origin
- Solve the same problems as previously by replacing the line with a hyperplane.
SVD and least-squares
- Consider the matrix
 formed as
formed as 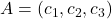 , with
, with
with ![]() a vector chosen randomly in
a vector chosen randomly in ![]() . In addition, we define
. In addition, we define
with again ![]() chosen randomly in
chosen randomly in ![]() . We consider the associated least-squares problem
. We consider the associated least-squares problem
-
- What is the rank of
 ?
? - Apply the least-squares formula
 . What is the norm of the residual vector,
. What is the norm of the residual vector, 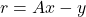 ?
? - Express the least-squares solution in terms of the SVD of
 . That is, form the pseudo-inverse of
. That is, form the pseudo-inverse of  and apply the formula
and apply the formula  . What is now the norm of the residual?
. What is now the norm of the residual? - Interpret your results.
- What is the rank of
- Consider a least-squares problem
where the data matrix ![]() has rank one.
has rank one.
-
- Is the solution unique?
- Show how to reduce the problem to one involving one scalar variable.
- Express the set of solutions in closed form.
