Exercises
Interpretation of covariance matrix
We are given ![]() of points
of points ![]() in
in ![]() . We assume that the average and variance of the data projected along a given direction do not change with the direction. In this exercise, we will show that the sample covariance matrix is then proportional to the identity.
. We assume that the average and variance of the data projected along a given direction do not change with the direction. In this exercise, we will show that the sample covariance matrix is then proportional to the identity.
We formalize this as follows. To a given normalized direction ![]() (
(![]() ), we associate the line with direction
), we associate the line with direction ![]() passing through the origin,
passing through the origin, ![]() . We then consider the projection of the points
. We then consider the projection of the points ![]() ,
, ![]() , on the line
, on the line ![]() , and look at the associated coordinates of the points on the line. These projected values are given by
, and look at the associated coordinates of the points on the line. These projected values are given by
We assume that for any ![]() , the sample average
, the sample average ![]() of the projected values
of the projected values ![]() ,
, ![]() , and their sample variance
, and their sample variance ![]() , are both constant, independent of the direction
, are both constant, independent of the direction ![]() (with
(with ![]() ). Denote by
). Denote by ![]() and
and ![]() the (constant) sample average and variance.
the (constant) sample average and variance.
Justify your answer to the following as carefully as you can.
- Show that

- Show that the sample average of the data points
is zero.
- Show that the sample covariance matrix of the data points,
is of the form ![]() , where
, where ![]() is the identity matrix of order
is the identity matrix of order ![]() . (Hint: the largest eigenvalue
. (Hint: the largest eigenvalue ![]() of the matrix
of the matrix ![]() can be written as:
can be written as: ![]() , and a similar expression holds for the smallest eigenvalue.)
, and a similar expression holds for the smallest eigenvalue.)
Eigenvalue decomposition
Let ![]() be two linearly independent vectors, with unit norm (
be two linearly independent vectors, with unit norm (![]() ). Define the symmetric matrix
). Define the symmetric matrix ![]() . In your derivations, it may be useful to use the notation
. In your derivations, it may be useful to use the notation ![]() .
.
- Show that
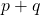 and
and 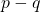 are eigenvectors of
are eigenvectors of  , and determine the corresponding eigenvalues.
, and determine the corresponding eigenvalues. - Determine the nullspace and rank of
 .
. - Find an eigenvalue decomposition of
 . Hint: use the previous two parts.
. Hint: use the previous two parts. - What is the answer to the previous part if
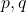 are not normalized?
are not normalized?
Positive-definite matrices, ellipsoids
- In this problem, we examine the geometrical interpretation of the positive definiteness of a matrix. For each of the following cases determine the shape of the region generated by the constraint
 .
.
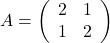 .
.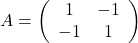 .
. .
.
- Show that if a square,
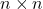 symmetric matrix
symmetric matrix  is positive semi-definite, then for every
is positive semi-definite, then for every 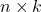 matrix
matrix 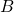 ,
, 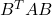 is also positive semi-definite. (Here,
is also positive semi-definite. (Here,  is an arbitrary integer.)
is an arbitrary integer.) - Drawing an ellipsoid. How would you efficiently draw an ellipsoid in
 , if the ellipsoid is described by a quadratic inequality of the form
, if the ellipsoid is described by a quadratic inequality of the form
where ![]() is
is ![]() and symmetric, positive-definite,
and symmetric, positive-definite, ![]() , and
, and ![]() ? Describe your algorithm as precisely as possible. (You are welcome to provide a Matlab code.) Draw the ellipsoid
? Describe your algorithm as precisely as possible. (You are welcome to provide a Matlab code.) Draw the ellipsoid
Least-squares estimation
- BLUE property of least-squares. Consider a system of linear equations in vector

where ![]() is a noise vector, and the input is
is a noise vector, and the input is ![]() , a full rank, tall matrix (
, a full rank, tall matrix (![]() ), and
), and ![]() . We do not know anything about
. We do not know anything about ![]() , except that it is bounded:
, except that it is bounded: ![]() , with
, with ![]() a measure of the level of noise. Our goal is to provide an estimate
a measure of the level of noise. Our goal is to provide an estimate ![]() of
of ![]() via a linear estimator, that is, a function
via a linear estimator, that is, a function ![]() with
with ![]() a
a ![]() matrix. We restrict attention to unbiased estimators, which are such that
matrix. We restrict attention to unbiased estimators, which are such that ![]() when
when ![]() . This implies that
. This implies that ![]() should be a left inverse of
should be a left inverse of ![]() , that is,
, that is, ![]() . An example of the linear estimator is obtained by solving the least-squares problem
. An example of the linear estimator is obtained by solving the least-squares problem
The solution is, when ![]() is full column rank, of the form
is full column rank, of the form ![]() , with
, with ![]() . We note that
. We note that ![]() , which means that the LS estimator is unbiased. In this exercise, we show that
, which means that the LS estimator is unbiased. In this exercise, we show that ![]() is the best unbiased linear estimator. (This is often referred to as the BLUE property.)
is the best unbiased linear estimator. (This is often referred to as the BLUE property.)
-
- Show that the estimation error of an unbiased linear estimator is
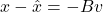 .
. - This motivates us to minimize the size of
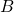 , say using the Frobenius norm:
, say using the Frobenius norm:
- Show that the estimation error of an unbiased linear estimator is
Show that ![]() is the best unbiased linear estimator (BLUE), in the sense that it solves the above problem. Hint: Show that any unbiased linear estimator
is the best unbiased linear estimator (BLUE), in the sense that it solves the above problem. Hint: Show that any unbiased linear estimator ![]() can be written as
can be written as ![]() with
with ![]() , and that
, and that ![]() is positive semi-definite.
is positive semi-definite.
