Determinant of a square matrix
Definition
The determinant of a square, ![]() matrix
matrix ![]() , denoted
, denoted ![]() , is defined by an algebraic formula of the coefficients of
, is defined by an algebraic formula of the coefficients of ![]() . The following formula for the determinant, known as Laplace’s expansion formula, allows to compute the determinant recursively:
. The following formula for the determinant, known as Laplace’s expansion formula, allows to compute the determinant recursively:
where ![]() is the
is the ![]() matrix obtained from
matrix obtained from ![]() by removing the
by removing the ![]() -th row and first column. (The first column does not play a special role here: the determinant remains the same if we use any other column.)
-th row and first column. (The first column does not play a special role here: the determinant remains the same if we use any other column.)
The determinant is the unique function of the entries of ![]() such that
such that
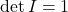 .
. is a linear function of any column (when the others are fixed).
is a linear function of any column (when the others are fixed). changes sign when two columns are permuted.
changes sign when two columns are permuted.
There are other expressions of the determinant, including the Leibnitz formula (proven here):
where ![]() denotes the set of permutations
denotes the set of permutations ![]() of the integers
of the integers ![]() . Here,
. Here, ![]() denotes the sign of the permutation
denotes the sign of the permutation ![]() , which is the number of pairwise exchanges required to transform
, which is the number of pairwise exchanges required to transform ![]() into
into ![]() .
.
Important result
An important result is that a square matrix is invertible if and only if its determinant is not zero. We use this key result when introducing eigenvalues of symmetric matrices.
Geometry
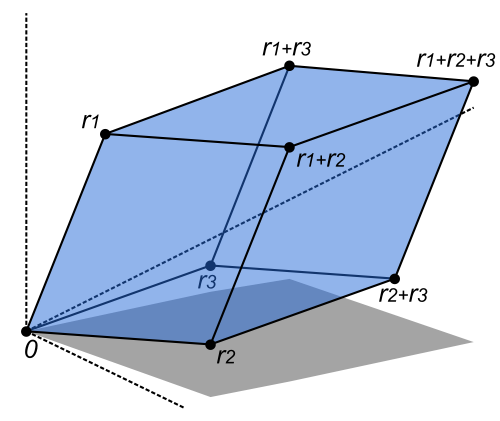 |
The determinant of a |
In general, the absolute value of the determinant of a ![]() matrix is the volume of the parallelepiped
matrix is the volume of the parallelepiped
This is consistent with the fact that when ![]() is not invertible, its columns define a parallepiped of zero volume.
is not invertible, its columns define a parallepiped of zero volume.
Determinant and inverse
The determinant can be used to compute the inverse of a square, full-rank (that is, invertible) matrix ![]() : the inverse
: the inverse ![]() has elements given by
has elements given by
, where ![]() is a matrix obtained from
is a matrix obtained from ![]() by removing its
by removing its 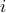 -th row and
-th row and 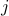 -th column. For example, the determinant of a
-th column. For example, the determinant of a ![]() matrix
matrix
is given by
It is indeed the volume of the area of a parallepiped defined with the columns of ![]() ,
, ![]() . The inverse is given by
. The inverse is given by
Some properties
Determinant of triangular matrices
If a matrix is square, triangular, then its determinant is simply the product of its diagonal coefficients. This comes right from Laplace’s expansion formula above.
Determinant of transpose
The determinant of a square matrix and that of its transpose are equal.
Determinant of a product of matrices
For two invertible square matrices, we have
In particular:
This also implies that for an orthogonal matrix ![]() , that is, a
, that is, a 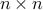 matrix with
matrix with ![]() , we have
, we have
Determinant of block matrices
As a generalization of the above result, we have three compatible blocks ![]() :
:
A more general formula is
