Definitions

L. El Ghaoui

Definitions

Symmetric matrices and quadratic functions
Second-order approximation of non-linear functions
Special symmetric matrices

Symmetric matrices and quadratic functions

Symmetric matrices

A square matrix $A \in \mathbb{R}^{n\times n}$ is symmetric if it is equal to its transpose. That is,

$A_{ij} = A_{ji}, \quad 1 \leq i,j \leq n.$

The set of symmetric $n \times n$ matrices is denoted ${\bf S}^n$ . This set is a subspace of $\mathbb{R}^{n\times n}$ .

Examples:

A $3 \times 3$ example.
Representation of a weighted, undirected graph.
Laplacian matrix of a graph.
Hessian of a function.
Gram matrix of data points.

Quadratic functions

A function $q: \mathbb{R}^n \rightarrow \mathbb{R}$ is said to be a quadratic function if it can be expressed as

$q(x) = \sum\limits_{i=1}^n \sum\limits_{j=1}^n A_{ij}x_ix_j+2\sum\limits_{i=1}^n b_ix_i+c,$

for numbers $A_{ij}$ , $b_i$ , and $c$ , $i,j \in \{1,\cdots,n\}$ . A quadratic function is thus an affine combination of the $x_i$ ‘s and all the ‘‘cross-products’’ $x_i x_j$ . We observe that the coefficient of $x_i x_j$ is $(A_{ij} + A_{ji})$ .

The function is said to be a quadratic form if there are no linear or constant terms in it: $b_i = 0$ , $c=0$ .

Note that the Hessian (matrix of second-derivatives) of a quadratic function is constant.

Examples:

Link between quadratic functions and symmetric matrices

There is a natural relationship between symmetric matrices and quadratic functions. Indeed, any quadratic function $q: \mathbb{R}^n \rightarrow \mathbb{R}$ can be written as

$q(x)=\left(\begin{array}{c} x \\ 1 \end{array}\right)^T\left(\begin{array}{cc} A & b \\ b^T & c \end{array}\right)\left(\begin{array}{c} x \\ 1 \end{array}\right)=x^T A x+2 b^T x+c,$

for an appropriate symmetric matrix $A \in {\bf S}^n$ , vector $b \in \mathbb{R}^n$ and scalar $c \in \mathbb{R}$ . Here, $A_{ii}$ is the coefficient of $x_i^2$ in $q$ ; for $i \neq j$ , $2A_{ij}$ is the coefficient of the term $x_i x_j$ in $q$ ; $2b_i$ is that of $x_i$ ; and $c$ is the constant term, $q(0)$ . If $q$ is a quadratic form, then $b=0$ , $c=0$ , and we can write $q(x) = x^TAx$ where now $A \in {\bf S}^n$ .

Examples:

Two-dimensional example.

Second-order approximations of non-quadratic functions

We have seen how linear functions arise when one seeks a simple, linear approximation to a more complicated non-linear function. Likewise, quadratic functions arise naturally when one seeks to approximate a given non-quadratic function by a quadratic one.

One-dimensional case

If $f: \mathbb{R} \rightarrow \mathbb{R}$ is a twice-differentiable function of a single variable, then the second-order approximation (or, second-order Taylor expansion) of $f$ at a point $x_0$ is of the form

$f(x) \approx q(x) = f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2}f''(x_0)(x-x_0)^2,$

where $f'(x_0)$ is the first derivative, and $f''(x_0)$ the second derivative, of $f$ at $x_0$ . We observe that the quadratic approximation $q$ has the same value, derivative, and second-derivative as $f$ , at $x_0$ .

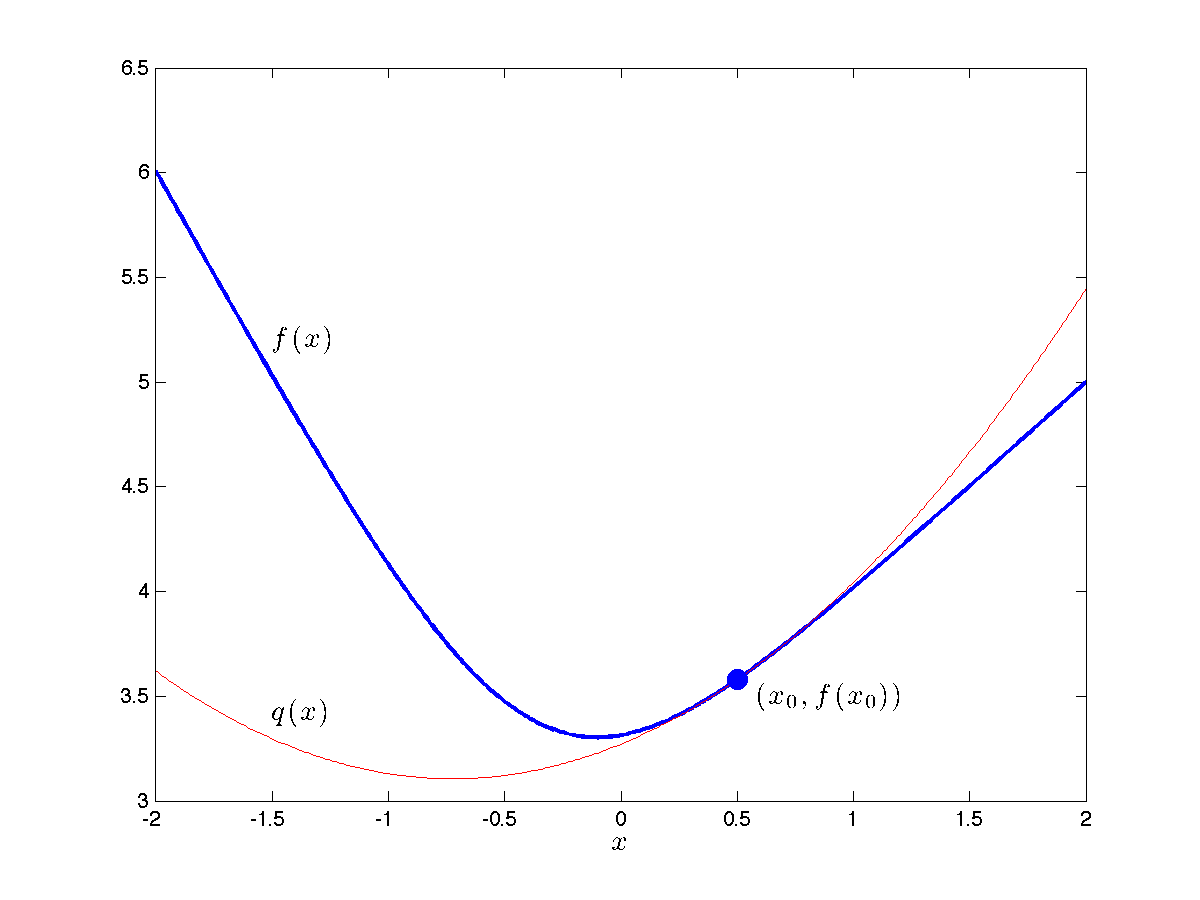Example: The figure shows a second-order approximation $q$ of the univariate function $f:\mathbb{R} \rightarrow \mathbb{R}$ , with values

$f(x) = \log(\exp(x-3)+\exp(-2x+2)),$

at the point $x_0 = 0.5$ (in red).

Multi-dimensional case

In multiple dimensions, we have a similar result. Let us approximate a twice-differentiable function $f: \mathbb{R}^n \rightarrow \mathbb{R}$ by a quadratic function $q$ , so that $f$ and $q$ coincide up and including to the second derivatives.

The function $q$ must be of the form

$q(x) = x^TAx+2b^Tx+c,$

where $A \in {\bf S}^n$ , $b \in \mathbb{R}^n$ , and $c \in \mathbb{R}$ . Our condition that $q$ coincides with $f$ up and including to the second derivatives shows that we must have

$\nabla^2 q(x)=2A=\nabla^2 f(x_0),\quad \nabla q(x) = 2(Ax_0+b) = \nabla f(x_0), \quad x^TAx_0+2b^Tx_0 + c = f(x_0),$

where $\nabla^2 f(x_0)$ is the Hessian, and $\nabla f(x_0)$ the gradient, of $f$ at $x_0$ .

Solving for $A,b,c$ we obtain the following result:

Second-order expansion of a function. The second-order approximation of a twice-differentiable function $f$ at a point $x_0$ is of the form

$f(x) \approx q(x) = f(x_0)+\nabla f(x_0)^T(x-x_0)+\frac{1}{2}(x-x_0)^T\nabla^2 f(x_0)(x-x_0),$

where $\nabla f(x_0) \in \mathbb{R}^n$ is the gradient of $f$ at $x_0$ , and the symmetric matrix $\nabla^2 f(x_0)$ is the Hessian of $f$ at $x_0$ .

Example: Second-order expansion of the log-sum-exp function.

Special symmetric matrices

Diagonal matrices

Perhaps the simplest special case of symmetric matrices is the class of diagonal matrices, which are non-zero only on their diagonal.

If $\lambda \in \mathbb{R}^n$ , we denote by ${\bf diag}(\lambda_1, \cdots, \lambda_n)$ , or ${\bf diag} (\lambda)$ for short, the $n \times n$ (symmetric) diagonal matrix with $\lambda$ on its diagonal. Diagonal matrices correspond to quadratic functions of the form

$q(x) = \sum\limits_{x=1}^n \lambda_i x_i^2 = x^T{\bf diag}(\lambda)x.$

Such functions do not have any ‘‘cross-terms’’ of the form $x_i x_j$ with $i \neq j$ .

Example: A diagonal matrix and its associated quadratic form.

Symmetric dyads

Another important class of symmetric matrices is that of the form $uu^T$ , where $u \in \mathbb{R}^n$ . The matrix has elements $u_i u_j$ and is symmetric. Such matrices are called symmetric dyads. (If $||u||_2=1$ , then the dyad is said to be normalized.)