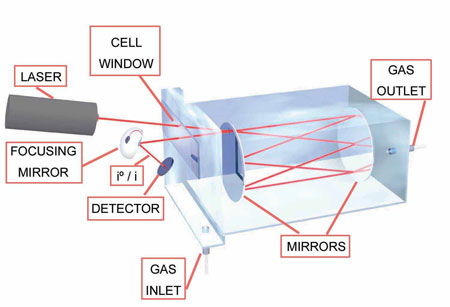
Beer-Lambert Law in Absorption Spectrometry

The Beer-Lambert law in optics is an empirical relationship that relates the absorption of light by a material, to the properties of the material through which the light is traveling. This is the basis of absorption spectrometry, which allows to measure the concentration of different gases in a chamber.

The principle of an absorption spectrometer, illustrated on the left, is as follows. Consider the following two experiments. First, we do a control experiment, where we illuminate from one side a container containing some reference gas with light at a certain frequency. We measure the light intensity (say, ) at the other side of the container. Then, we add some other gas to the container, repeat the experiment, and measure the light intensity again (say, ). Depending on the absorption properties, as well as the concentration , of the added gas, the light will be more or less absorbed with respect to the reference situation. The Beer-Lambert law postulates that the log-ratio is linear in the concentration . In other words, , where the constant depends on the light frequency and on the gas.

If the container has a mixture of ‘‘pure’’ gases in it, the law postulates that the logarithm of the ratio of the light intensities is a linear function of the concentrations of each gas in the mix. The log-ratio of intensities is thus of the form for some vector , where is the vector of concentrations. The coefficients , correspond to the log-ratio of light intensities when (the -th vector of the standard basis, which correspond to the -th pure gas). The quantity is called the coefficient of absorption of the -th gas and can be measured in the laboratory.

See also: Absorption spectrometry: using measurements at different light frequencies.