Basis in high dimension
The set of three vectors in ![]() :
:
(1) 
(2) 
(3) 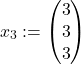
is not independent, since ![]() , and its span has dimension
, and its span has dimension ![]() . Since
. Since ![]() are independent (the equation
are independent (the equation ![]() has
has ![]() as the unique solution), a basis for that span is, for example,
as the unique solution), a basis for that span is, for example, ![]() . In contrast, the collection
. In contrast, the collection ![]() spans the whole space
spans the whole space ![]() , and thus forms a basis of that space.
, and thus forms a basis of that space.
