Basics
- Matrices as collections of column vectors
- Transpose
- Matrices as collections of row vectors
- Sparse matrices
Matrices as collections of column vectors
Matrices can be viewed simply as a collection of (column) vectors of same size, that is, as a collection of points in a multi-dimensional space.
Matrices can be described as follows: given ![]() vectors
vectors ![]() in
in ![]() we can define the
we can define the ![]() matrix
matrix ![]() with
with ![]() s as columns:
s as columns:
![]()
Geometrically, ![]() represents
represents ![]() points in a
points in a ![]() -dimensional space. The notation
-dimensional space. The notation ![]() denotes the set of
denotes the set of ![]() matrices.
matrices.
With our convention, a column vector in ![]() is thus a matrix in
is thus a matrix in ![]() , while a row vector in
, while a row vector in ![]() is a matrix in
is a matrix in ![]() .
.
Transpose
The notation ![]() denotes the element of
denotes the element of ![]() sitting in row
sitting in row ![]() and column
and column ![]() . The transpose of a matrix
. The transpose of a matrix ![]() denoted by
denoted by ![]() , is the matrix with
, is the matrix with ![]() element
element ![]() ,
, ![]() and
and ![]() .
.
Matrices as collections of rows
Similarly, we can describe a matrix in row-wise fashion: given ![]() vectors
vectors ![]() in
in ![]() , we can define the
, we can define the ![]() matrix
matrix ![]() with the transposed vectors
with the transposed vectors ![]() as rows:
as rows:
![Rendered by QuickLaTeX.com \[B = \begin{pmatrix} b_{1}^{T} \\ b_{2}^{T} \\ \vdots \\ b_{m}^{T} \end{pmatrix}.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6dcc8029868d2c0f52b1e8ccf6cad41e_l3.png)
Geometrically, ![]() represents
represents ![]() points in a
points in a ![]() -dimensional space.
-dimensional space.
>> A = [1 2 3; 4 5 6]; % a 2x3 matrix >> B = A'; % this is the transpose of matrix A >> B = [1 4; 2 5; 3 6]; % B can also be declared that way >> C = rand(4,5); % a random 4x5 matrix
Examples:
- A simple
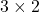 matrix.
matrix. - Arc-node incidence matrix of a network.
- Matrix of votes in the US Senate, 2004-2006.
Sparse Matrices
In many applications, one has to deal with very large matrices that are sparse, that is, they have many zeros. It often makes sense to use a sparse storage convention to represent the matrix.
One of the most common formats involves only listing the non-zero elements, and their associated locations ![]() in the matrix. In Matlab, the function
in the matrix. In Matlab, the function sparse allows to create a sparse matrix based on that information. The user needs also to specify the size of the matrix (it cannot infer it from just the above information).
>> S = sparse([3 2 3 4 1],[1 2 2 3 4],[1 2 3 4 5],4,4) % creates a 4x4 matrix >> S = [0 0 0 5; 0 2 0 0; 1 3 0 0; 0 0 4 0]; % the same matrix with ordinary convention
