Applications of SVD: market data analysis

We consider the daily log-returns of a collection of stocks chosen in the Fortune 100 companies over the time period from January 3, 2007, until December 31, 2008. We can represent this as a 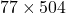 matrix, with each column a day, and each row a time-series corresponding to a specific stock.

The image on the left represents the time series of the stock market mentioned above, shown as a collection of time series. We note that the log-returns hover around a mean which appears to be close to zero.

We can form the SVD of the matrix of log returns, and plot the explained variance. We see that the first 10 singular values explain more than 80% of the data’s variance.

It is instructive to look at the singular vector corresponding to the largest singular value, arranged in increasing order. We observe that all the components have the same sign (which we can always assume is positive). This means we can interpret this vector as providing a weighted average of the market. As seen in the previous plot, the corresponding rank-one approximation roughly explains more than 80% of the variance in this market data, which justifies the phrase ‘‘the market average moves the market’’. The five components with the largest magnitude correspond to the following companies. Note that all are financial: FABC (Fidelity Advisor) FTU (Wachovia, bought by Wells Fargo) MER (Merrill Lynch, bought by Bank by America) AIG (don’t need to elaborate) MS (Morgan Stanley)