Applications of SVD: image compression

Images as matrices

We can represent images as matrices, as follows. Consider an image having pixels. For gray-scale images, we need one number per pixel, which can be represented as a matrix. For color images, we need three numbers per pixel, for each color: red, green, and blue (RGB). Each color can be represented as a matrix, and we can represent the full-color image as a  matrix, where we stack each color’s matrix column-wise alongside each other, as .

The image on the left is a grayscale image, which can be represented as a  matrix containing the gray-scale values stored as integers.

The image can be visualized in Matlab as well. We must first transform the matrix from integer to double. In JPEG format, the image will be loaded into Matlab as a three-dimensional array, with one matrix for each color. For gray-scale images, we only need the first matrix in the array.

>> A = imread(baboon-grayscale.jpg); % loads image in integer format as a 3d-array
>> A = double(A); % transform to real values
>> A = A(:,:,1); % for gray-scale images, we consider only the first matrix in the array

Low-rank approximation

Using the low-rank approximation via SVD method, we can form the best rank-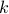 approximations for the matrix. The matlab code for this is as follows.

>> [U,S,V] = svd(A);
>> Ak = U(:,1:k)*S(1:k,1:k)*V(:,1:k)';

True and approximated images, with varying ranks. We observe that with , the approximation is almost the same as the original picture, whose rank is .

Recall that the explained variance of the rank- approximation is the between the squared norm of the error matrix, to the

The explained variance for the various rank- approximations to the original image. For , the approximation contains more than of the total variance in the picture.