A two-dimensional toy optimization problem
As a toy example of an optimization problem in two variables, consider the problem
(Note that the term ‘‘subject to’’ has been replaced with the shorthand colon notation.)
The problem can be put in standard form
where:
- the decision variable is
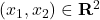 ;
; - the objective function
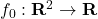 , takes values
, takes values
- the constraint functions
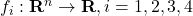 take values
take values
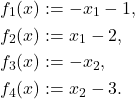
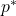 is the optimal value, which turns out to be
is the optimal value, which turns out to be 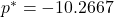 .
.
See also:
