A two-dimensional toy optimization problem

L. El Ghaoui

A two-dimensional toy optimization problem

As a toy example of an optimization problem in two variables, consider the problem

$\min _x 0.9 x_1^2-0.4 x_1 x_2-0.6 x_2^2-6.4 x_1-0.8 x_2:-1 \leq x_1 \leq 2, \quad 0 \leq x_2 \leq 3 .$

(Note that the term ‘‘subject to’’ has been replaced with the shorthand colon notation.)

The problem can be put in standard form

$p^*:=\min _x f_0(x): f_i(x) \leq 0, \quad i=1, \ldots, m,$

where:

the decision variable is $\left(x_1, x_2\right) \in \mathbf{R}^2$ ;
the objective function 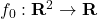$f_0: \mathbf{R}^2 \rightarrow \mathbf{R}$ , takes values

$f_0(x):=0.9 x_1^2-0.4 x_1 x_2-0.6 x_2^2-6.4 x_1-0.8 x_2 ;$

the constraint functions 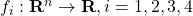$f_i: \mathbf{R}^n \rightarrow \mathbf{R}, i=1,2,3,4$ take values

$\begin{aligned} & f_1(x):=-x_1-1, \\ & f_2(x):=x_1-2, \\ & f_3(x):=-x_2, \\ & f_4(x):=x_2-3 . \end{aligned}$

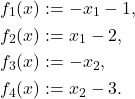
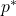$p^*$ is the optimal value, which turns out to be $p^*=-10.2667$ .
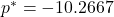The optimal set is the singleton 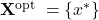$\mathbf{X}^{\text {opt }}=\left\{x^*\right\}$ , with

$x^*=\left(\begin{array}{c} 2.00 \\ 1.33 \end{array}\right) .$

Since the optimal set is not empty, the problem is attained.

We can represent the problem in epigraph form, as

$\min _{x, t} t: t \geq 0.9 x_1^2-0.4 x_1 x_2-0.6 x_2^2-6.4 x_1-0.8 x_2, \quad-1 \leq x_1 \leq 2, \quad 0 \leq x_2 \leq 3 .$

Geometric view of the toy optimization problem above. The level curves (curves of constant value) of the objective function are shown. The problem amounts to find the smallest value of $t$ such that $t=f_0(x)$ for some feasible $x$ . The plot also shows the unconstrained minimum of the objective function, located at $\hat{x}=(4,2)$ . An $\epsilon$ -sub-optimal set for the toy problem above is shown (in a darker color), for $\epsilon=0.9$ . This corresponds to the set of feasible points that achieves an objective value less or equal to $p^*+\epsilon$ .

A two-dimensional toy optimization problem

License

Share This Book