Sample covariance matrix

L. El Ghaoui

Sample covariance matrix

Definition

For a vector $z \in \mathbb{R}^m$ , the sample variance $\sigma^2$ measures the average deviation of its coefficients around the sample average $\hat{x}$ :

$\hat{z}:=\frac{1}{n}(z(1)+\ldots+z(m)), \quad \sigma^2:=\frac{1}{n}\left((z(1)-\hat{z})^2+\ldots+(z(m)-\hat{z})^2\right),$

Now consider a matrix $X = [x_1, \cdots, x_m] \in \mathbb{R}^{n\times m}$ , where each column $x_i$ represents a data point in $\mathbb{R}^n$ . We are interested in describing the amount of variance in this data set. To this end, we look at the numbers we obtain by projecting the data along a line defined by the direction $u \in \mathbb{R}^n$ . This corresponds to the (row) vector in $\mathbb{R}^m$ .

$z = (u^Tx_1, \cdots, u^T x_m) = u^TX\in \mathbb{R}^m.$

The corresponding sample mean and variance are

$\hat{z} = u^T \hat{x}, \quad \sigma^2(u):= \frac{1}{m} \sum\limits_{k=1}^m (u^Tx_k - u^T \hat{x})^2,$

where $\hat{x} := (1/m)(x_1 + \cdots + x_m) \in \mathbb{R}^n$ is the sample mean of the vectors $x_1, \cdots, x_m$ .

The sample variance along direction $u$ can be expressed as a quadratic form in $u$ :

$\sigma^2(u) = \frac{1}{n} \sum\limits_{k=1}^n [u^T(x_k-\hat{x}]^2 = u^T\sum u,$

where $\sum$ is a $n \times n$ symmetric matrix, called the sample covariance matrix of the data points:

$\sum: = \frac{1}{m} \sum\limits_{k=1}^m (x_k-\hat{x})(x_k - \hat{x})^T.$

Properties

The covariance matrix satisfies the following properties.

The sample covariance matrix allows finding the variance along any direction in data space.
The diagonal elements of 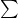$\sum$ give the variances of each vector in the data.
The trace of 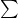$\sum$ gives the sum of all the variances.
The matrix 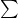$\sum$ is positive semi-definite, since the associated quadratic form 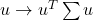$u \rightarrow u^T\sum u$ is non-negative everywhere.

Matlab syntax

The following matlab syntax assumes that the $m$ data points in $\mathbb{R}^n$ are collected in a $n\times m$ matrix $X$ : $X = [x_1, \cdots, x_m]$ .

Matlab syntax

>> xhat = mean(X,2); % mean of columns of matrix X
>> Xc = X-xhat*ones(1,m); % centered data matrix
>> Sigma = (1/m)*Xc'*Xc; % covariance matrix
>> Sigma = cov(X',1); % built-in command produces the same thing

Sample covariance matrix

Definition

Properties

Matlab syntax

License

Share This Book