2.2 The Physiology of a Mechanically Delivered Breath

Once someone is intubated and attached to a ventilator, the lungs are now a “sealed system.” This means that whatever air is pushed out of the ventilator has nowhere else to go except into the lungs (inhalation), and air that leaves the lungs has nowhere to go except for back to the ventilator (exhalation).

In the case of mechanical ventilation, inspiration occurs by air being pushed from the ventilator into the lungs by creating positive pressure at the mouth. Inspiration continues until the breath has been fully given—either what is set by the ventilator (mandatory/control breaths) or based on the patient demand (spontaneous breaths).

In this scenario, inspiration is triggered by the application of positive pressure at the mouth through the ventilator, rather than by the contraction of the diaphragm and the creation of negative pressure, as observed during a spontaneous breath. This positive pressure delivered by the ventilator initiates the inflow of air into the lungs. At the beginning of inspiration pressure is applied at the mouth making [latex]P_m[/latex] positive, compared to [latex]P_{alv}[/latex], which is zero at this point (or less than [latex]P_m[/latex]). This results in a pressure gradient, and air flows into the alveoli following a positive transairway pressure gradient. [latex]\text{PTA}=P_m-P_{alv}[/latex].

As the lungs inflate, [latex]P_{alv}[/latex] becomes progressively more positive ([latex]P_{alv}[/latex] Increases). Under normal circumstances—in healthy lungs—at the end of inspiration, when tidal volume is delivered, these pressures equilibrate [latex](P_{alv}=P_m)[/latex]. The positive pressure in the lungs is now transmitted to the pleural space resulting in [latex]P_{pl}[/latex] becoming more positive. This effect can cause physiological changes and even complication, deepening on lung compliance and resistance and the state of the cardiovascular system. These complications will be addressed in a later chapter. Positive pressure breathing attempts to inflate the lungs by increasing transpulmonary pressure gradient.

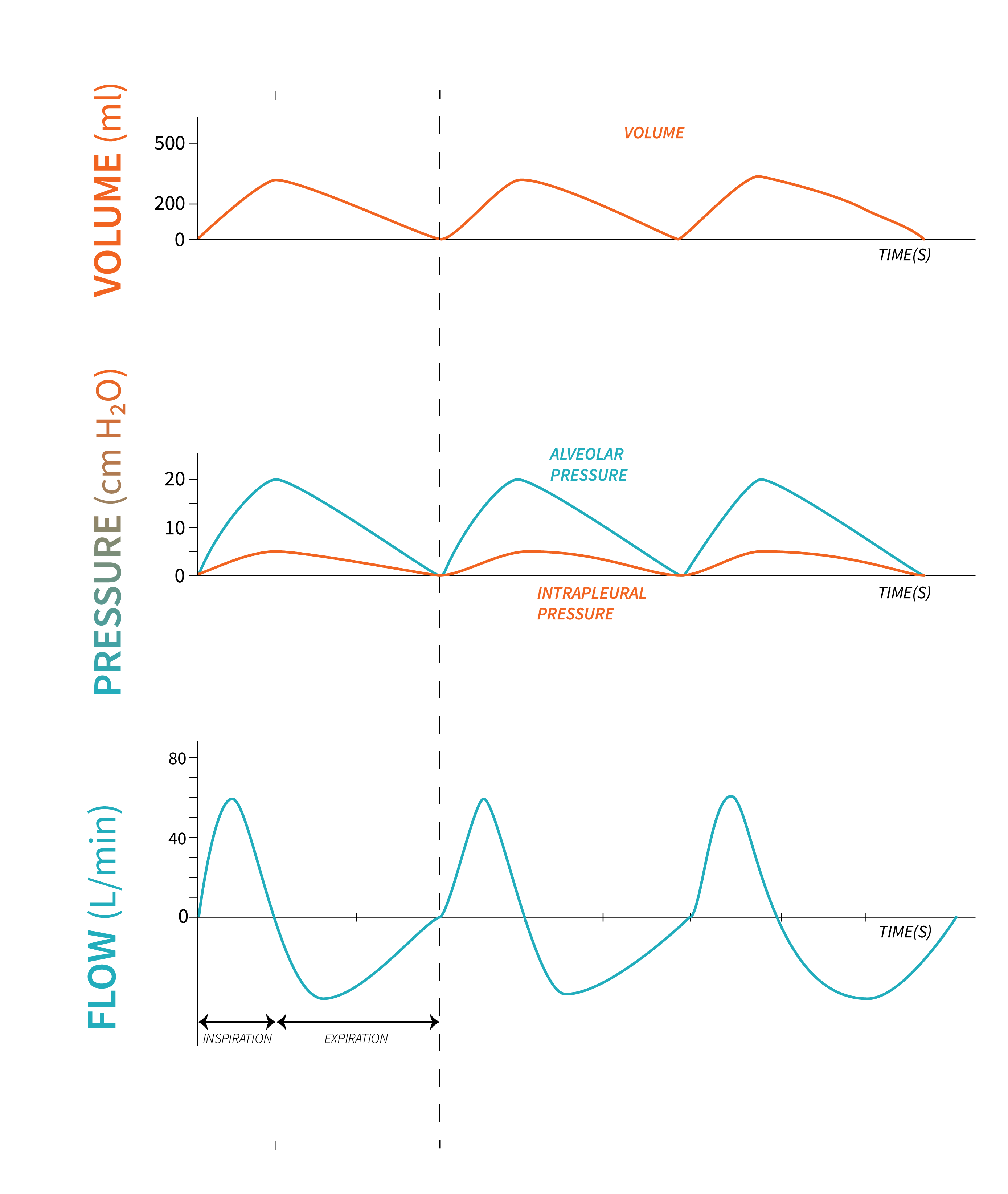
When full, the inflated lungs have a higher pressure than the outside atmosphere once the driving pressure stops from the ventilator. At the end of inspiration, the ventilator stops delivering positive pressure. Exhalation remains a passive process and it begins when a valve opens (exhalation valve), and the ventilator allows the air to flow through a filter out to atmosphere—the full alveoli will be higher pressure than the atmosphere, similar to the concept of spontaneous breathing where, during exhalation, the pressure in the lungs is higher than the pressure at the mouth ([latex]P_m[/latex]). Air flows from high to low pressure from the lungs back to the ventilator.

Apply Your Learning

Refer to the following diagram of a patient who requires a mechanical ventilator (Figure 2.2.2). Can you understand why the mechanical ventilator is a sealed system? It is also a good idea to start becoming familiar with the parts of the ventilator. You’ll learn a lot more about them in future chapters.

Lung mechanics and Definition of Pressures in Positive Pressure Ventilation

During Positive Pressure Ventilation (PPV), pressures in the lungs are continuously monitored and displayed on the ventilator screen (PPV). Let’s examine a graphic representation of pressures in the lungs at various points in the respiratory cycle, during positive pressure ventilation (Figure 2.2.3).

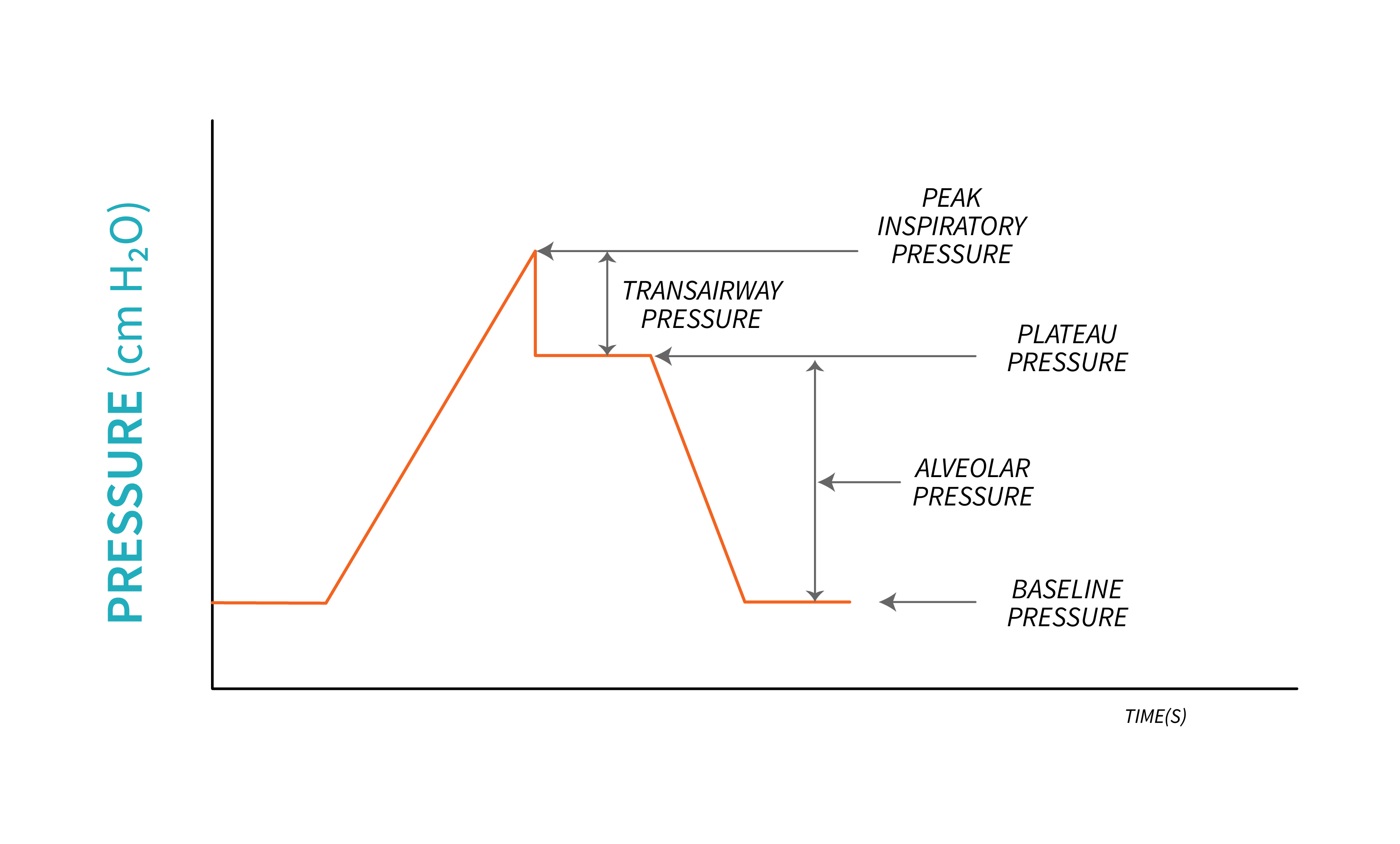
Baseline Pressure

Similar to spontaneous breathing, pressures are referenced to a baseline pressure during PPV. This pressure is exerted by the volume of air left in the lungs at the end of an expiration. We learned in Chapter 1 that this is the Functional Residual Capacity (FRC), or when positive pressure is applied, Positive End-Expiratory Pressure (PEEP). As the name suggests, during PPV, we often select a baseline pressure that is higher than zero (atmospheric pressure). When PEEP is set on a ventilator, the volume of air remaining in the lungs at the end of an exhalation is increased. PEEP added through the ventilator increases FRC and is called Extrinsic PEEP. A potential complication of PPV is air trapped in the lungs, most often when a patient does not have enough time to exhale completely is Intrinsic PEEP or Auto-PEEP.

Peak Inspiratory Pressure

As inspiration begins, and air flows into the lungs, pressure increases progressively, reaching its highest point at the end of inspiration. This is called Peak Inspiratory Pressure (PIP). The pressure required to inflate the lung is the distending pressure, or alveolar pressure.

Plateau Pressure

This pressure is a measure of the compliance of the lungs and it depends on the passive recoil of the lungs, and it is used frequently as part of assessment of ventilated patients. It is measured under static conditions, when flow stops, at the end of an inspiration, with the ventilator performing an inspiratory hold before expiration begins. This Inspiratory hold lasts between [latex]0.5[/latex] to [latex]1.5\text{ seconds}[/latex], while the ventilator prevents the exhalation valve from opening to allow exhalation. At the end of an inspiration, during a breath hold, flow stops as the gradient between pressure at the airway opening ([latex]P_{ao}[/latex]) is equal to the pressure in the alveoli ([latex]P_{alv}[/latex]). [latex]P_{ao}=P_{alv}[/latex]. During this time, the pressure in the lungs is determined by the the elastic recoil of the lungs and relaxation of respiratory muscles, and it stabilizing to a plateau because there is no air movement. It is measured by the ventilator as plateau pressure ([latex]P_{plat}[/latex]). Note that, if the patient is actively breathing during this inspiratory hold, a plateau will most likely not be obtained and may lead to inadequate measurements.

From the pressure-time graphics above, you will notice that the peak inspiratory pressure is the sum of the pressure required to overcome the resistance to flow through the airways (transairway pressure, [latex]P_{TA}[/latex]), the pressure required to inflate alveoli, and the pressure already present in the lung—baseline pressure.

Using the equation of motion, we can describe the dynamics of breathing and examine the differences between spontaneous breaths, negative breaths, and positive breaths, as well as the factors that impact the movement airflow into and out of the lungs.

[latex]P_{mus}+P_{vent}=P_E+P_R[/latex]

Going back to the idea that the patient connected to the ventilator is a sealed system, the equation of motion help describe the interactions between ventilator and lungs. This equation is basically a mathematical representation of the relationship between pressure, volume, and flow in the lungs, where muscle pressure together with ventilator pressure, equal elastic recoil pressure and resistance to flow pressure. This will help us better understand the dynamics of breathing during positive pressure ventilation under various pathophysiological conditions. The left side of the equation, [latex](P_{mus}+P_{vent})[/latex], describes the pressure required to inflate the lungs, with a dynamic component, the transairway pressure, required to overcome resistance to flow in the conducting airways, and a static component, alveolar pressure, which will maintain lung inflation. This is simply the Peak Inspiratory Pressure (PIP) described above.

For a non-ventilated patient, this pressure, ([latex]P_{mus}[/latex]), is provided by the contraction of respiratory muscles. For a ventilated patient, the ventilator will provide the remaining power needed for a breath ([latex]P_{vent}[/latex]) depending on their ability to generate partial pressure by contraction of respiratory muscles.

The right side of the equation describes the factors that oppose lung inflation.

Resistive pressure [latex]P_R[/latex], the dynamic element opposing lung inflation describes the pressure required to overcome the resistance to flow through the conducting airways, which we learned in Chapter 1. This is also called transairway pressure, [latex]P_{TA}[/latex]. The relationship between transairway pressure, resistance and flowrate can be written as:

[latex]P_{TA}=R \times\dot V[/latex]

Elastic recoil pressure, [latex]P_E[/latex], the static component that opposes lung inflation, is the pressure required to inflate the lungs with a certain volume based on elastance (a measure of lung stiffness). This is also called alveolar distending pressure ([latex]P_{alv}[/latex]) and it illustrates how changes in lung volume can affect the elastic recoil pressure generated by the lungs. We learned in Chapter 1 that compliance ([latex]C[/latex]) is the reciprocal of elastance ([latex]E[/latex]). [latex]E=\frac1{C}[/latex] and the pressure required to inflate the lung is alveolar pressure [latex]P_{alv}[/latex]. Therefore, we can write the relationship between the pressure exerted by the elastic recoil of the lungs, the elastance and the volume of air present in the lungs as follows:

[latex]P_{alv}=\frac{V}{C}[/latex]

So, to inflate the lungs, the pressure generated by respiratory muscles and/or ventilator must be equal to the sum of the pressures required to overcome compliance and resistance of the lungs. The equation of motion can be rewritten:

[latex]P_{mus}+P_{vent}=P_{alv}+P_{TA}[/latex]

“The Physiology of a Mechanically Delivered Breath“ from Basic Principles of Mechanical Ventilation by Melody Bishop, © Sault College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.