1.4 Ventilation
The Respiratory Cycle
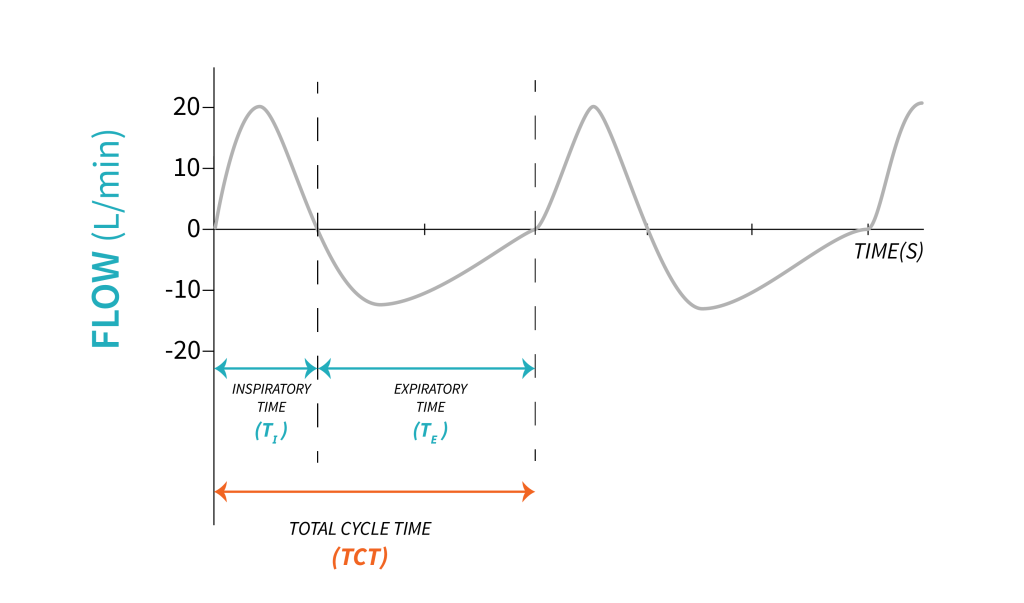
When we talk about ventilation, we refer to the cyclic movement of air between atmosphere and alveoli. With every inspiration, we move a volume of air, called tidal volume ([latex]V_T[/latex]), from ambient into the alveoli, and with every expiration we remove that tidal volume of air from the alveoli back to the ambient. The time required for this process is called total cycle time (TCT). In healthy adults, the average tidal volume at rest is approximately [latex]500\text{ mL}[/latex], although this can vary depending on factors such as age, sex, height, weight, and physical activity level. During exercise or other physical exertion, tidal volume can increase to facilitate increased oxygen uptake and carbon dioxide elimination.
Key Takeaway
Tidal volume refers to the volume of air that is inhaled or exhaled during a single breath in normal breathing. It is the amount of air that moves in and out of the lungs with each respiratory cycle, and is typically measured in milliliters (mL) or liters (L).
Under normal physiological circumstances, lungs move tidal volume 12-18 times per minute. This is normal respiratory rate ([latex]RR[/latex]).
The timing of one respiratory cycle can be divided into inspiratory time ([latex]T_I[/latex]), time required for inspiration, and expiration time ([latex]T_E[/latex]), time required for expiration. In mechanical ventilation, the relationship between inspiration and expiration is often expressed as a ratio [latex]\text{I:E}[/latex] and it can be determined easily when inspiratory and expiratory times are known.
Let’s calculate the [latex]\text{I:E}[/latex] ratio for an adult individual breathing with an inspiration of 2 seconds and an expiration of 4 seconds.
[latex]TCT=T_I+T_E[/latex]
[latex]TCT=2\text{ s}+4\text{ s}=6\text{ s}[/latex]
[latex]\text{I:E}=2:4[/latex]
[latex]\text{I:E}=1:2[/latex]
In mechanical ventilation, in the [latex]\text{I:E}[/latex] ratio, the numerator is always expressed as 1 (divide the numerator by itself). In this example, we divide the numerator, 2, by 2. To keep the ratio constant, we divide the denominator by 2 as well. In other words, we simplified the ratio.
Key Takeaway
Total cycle time is a function of respiratory rate per minute [latex](1\text{ min}=60\text{ s})[/latex]:
[latex]\frac{60\text{ s}}{RR}=TCT[/latex]
Example:
For a rate of 15 breaths/min, TCT is 4 s
[latex]\frac{60\text{ s}}{15}=4\text{ s}[/latex]
Minute Ventilation
The product of respiratory rate and tidal volume, expressed in litres per minute, is the total volume of air moving in and out of the lungs. This total volume is called minute ventilation ([latex]V_E[/latex]), and it is an important element that we will be using often as we learn more about mechanical ventilation.
Object Lesson
Minute Ventilation: [latex]V_E\;\left(\frac{\text{L}}{\text{min}}\right)[/latex]
[latex]V_E=RR\times V_T[/latex]
For an adult individual, breathing at a respiratory rate of 15 breaths per minute, with a tidal volume of [latex]500\text{ mL}[/latex]:
[latex]V_E=15\frac{\text{breaths}}{\text{min}}\times 500\text{ mL}[/latex]
[latex]V_E=7500\frac{\text{mL}}{\text{min}}[/latex]
Expressed in [latex]\frac{\text{L}}{\text{min}}[/latex]: [latex]7500\frac{\text{mL}}{\text{min}}=7.5\frac{\text{L}}{\text{min}}[/latex] [latex](1\text{ L}=1000\text{ mL})[/latex]
[latex]V_E[/latex] for this individual is [latex]7.5\frac{\text{L}}{\text{min}}[/latex]
Alveolar ventilation
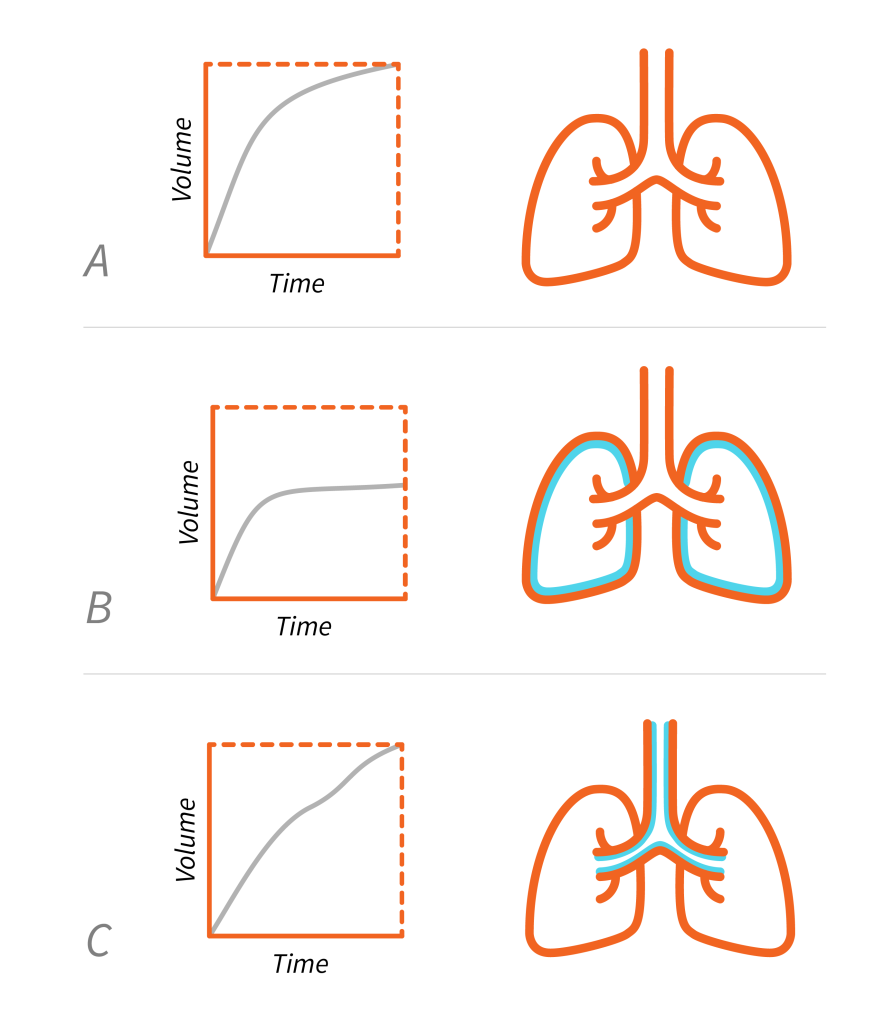
Alveolar ventilation describes the total volume of air moving in and out of the lungs, including the volume of dead space. In the context of mechanical ventilation, dead space refers to the portion of the tidal volume that does not participate in gas exchange. This occurs when air is inhaled into the anatomical dead space ([latex]V_{Danat}[/latex]) of the respiratory system, which includes the trachea, bronchi, and bronchioles, but does not reach the alveoli where gas exchange occurs. Anatomical dead space is usually [latex]1\text{ mL/lb}[/latex]. Ideal body weight is [latex](2.2\text{ mL/Kg})[/latex].
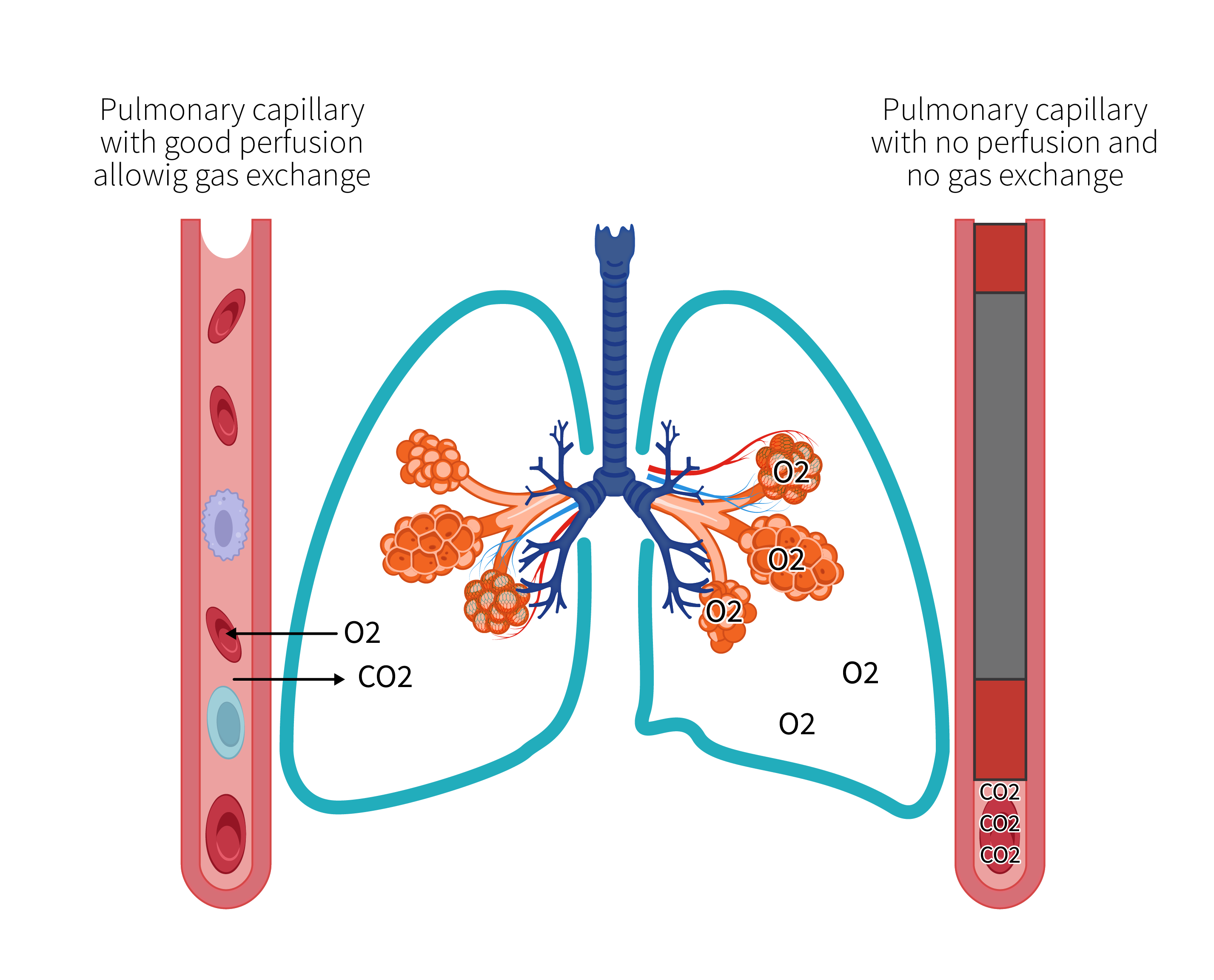
Alveolar dead space ([latex]V_{Dalv}[/latex]) refers to areas of the lung where gas exchange is impaired due to ventilation-perfusion mismatch or decreased blood flow, resulting in air being inhaled and exhaled without exchanging oxygen and carbon dioxide. These areas of the lung are ventilated, but not perfused or poorly perfused with mixed venous blood, resulting in poor gas exchange.
Imagine oxygen and carbon dioxide molecules as people waiting at a bus stop. Just as waiting at a bus stop without a bus prevents people from reaching their desired destination, impaired alveolar ventilation limits the proper exchange of oxygen and carbon dioxide in the lungs in the absence of or reduced blood flow. This is a situation where airflow occurs, but the gas exchange process within the alveoli doesn't happen as expected.
 |
 |
The sum of anatomical dead space and alveolar dead space determines the physiological dead space [latex](V_{D\;phys})[/latex]:
[latex]V_{Dphys}=V_{Danat}+V_{Dalv}[/latex]
Physiological dead space can be used to determine the efficiency of ventilation.
[latex]V_A=RR(V_T-V_{Dphys})[/latex]
In clinical practice, using data obtained from bedside monitoring, physiological dead space is often expressed as a ratio to tidal volume ([latex]\frac{V_D}{V_T}[/latex]).
Lung Compliance
A simple definition describes compliance as the change in volume per change in pressure, and it is measured in [latex]\frac{\text{mL}}{\text{cmH}_2\text{O}}[/latex].
[latex]C=\frac{\Delta V}{\Delta P}[/latex]
Compliance is the reciprocal of elastance ([latex]C=\frac1{E}[/latex]) and is the result of the elastic forces and surface tension that oppose lung inflation. The surface of each alveolus experiences tension in the absence of any other forces. This surface tension arises from cohesive forces between liquid molecules at the air-liquid interface within the alveoli. Imagine each alveolus as a miniature sphere that expands and contracts independently in all directions, pressing against adjacent alveoli. In order to expand the millions of alveoli in the lungs, a specific amount of inflation pressure is necessary. This is the elastic recoil pressure, also called distending pressure, and it becomes greater as the alveolar radius decreases, as explained by LaPlace's Law. To prevent the collapse of alveoli, which require a significant amount of pressure to reopen, pulmonary surfactant is released to decrease the surface tension within the alveoli as the radius decreases. In conditions where pulmonary surfactant is reduced or absent, such as certain diseases, high ventilating pressures may be necessary, which can potentially cause harm to the lungs. Because the lungs consist of elastic tissue, they tend to empty on their own when unobstructed, much like an untied balloon that gradually deflates due to the principles of Hooke's law of elasticity.
LaPlace's Law
LaPlace's Law: [latex]P=\frac{2ST}{R}[/latex]
Where:
[latex]ST=\text{Surface tension }(\frac{\text{dyne}}{\text{cm}^3})[/latex]
[latex]P=\text{pressure acting against the surface tension}(\frac{\text{dyne}}{\text{cm}^2})[/latex]
[latex]R=\text{radius of the sphere}[/latex]
Object Lesson
A balloon that is easy to inflate, is considered compliant (with reduced elasticity). This balloon can be described as more compliant, less elastic.
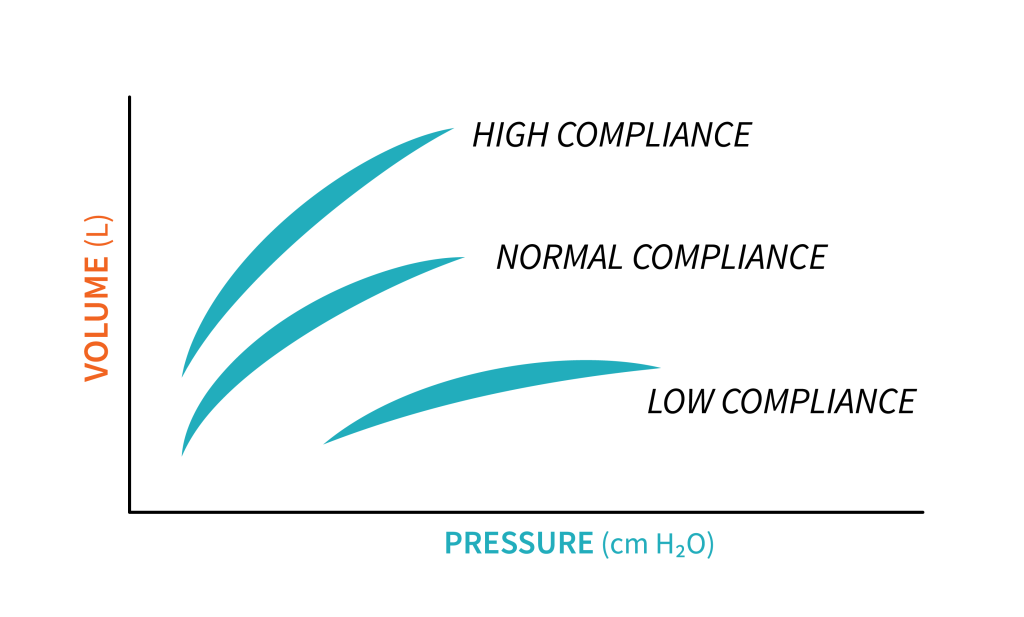
In clinical practice, you may come across various pathological conditions that affect the compliance of the lungs. Pulmonary fibrosis, for instance, can cause a decrease in compliance, resulting in minimal volume changes for any given change in pressure. Conversely, emphysema can cause an increase in compliance due to a loss of tissue elasticity. Generally, the respiratory system has a total compliance of approximately [latex]100\frac{\text{mL}}{\text{cmH}_2\text{O}}[/latex], with a range of [latex]50\text{ - }170\frac{\text{mL}}{\text{cmH}_2\text{O}}[/latex]. This total compliance is comprised of two main components: lung compliance and chest wall compliance, both of which play a crucial role in the elastic behaviour of the respiratory system.
Key Takeaway
Compliance varies with changing conditions such as patient position, respiratory effort and disease process. Any change in lung or chest wall conditions, or both, will affect the total compliance of the respiratory system and the pressure required to inflate the lungs.
A graphic representation of change in volume over change in pressure describes the compliance curve. As described above, you will notice that the position of the curve varies with conditions of the respiratory system. The compliance curve of a patient with emphysema is shifted to the left, compared to a normal compliance curve, as less pressure is required to inflate the lung. The compliance curve of a patient with lung fibrosis will be shifted to the right compared to the normal compliance curve, as more pressure is required to inflate the lung. Monitoring compliance is a critical parameter in mechanical ventilation, as it provides valuable information that can guide adjustments to the ventilator settings and improve patient outcomes.
Check Your Knowledge
Answer
Airway resistance
As air enters the lungs through the conducting airways, it experiences frictional forces, resulting in a resistance to flow known as airway resistance. This resistance can be quantified as the amount of pressure needed to overcome the frictional forces that oppose the inflation of the lungs. The pressure required to overcome this resistance is what we described earlier as transairway pressure ([latex]P_{TA}[/latex]). Air movement caused by lung and chest wall movement during breathing also encounters resistance as a result of the viscous resistance of lung tissue and surrounding tissues and organs. This viscous tissue resistance generally remains constant under normal circumstances and it represents about [latex]20\%[/latex] of total resistance. Viscous resistance may increase in certain pathological conditions such as ascites and obesity. Airway resistance represents about [latex]80\%[/latex] of total resistance. Under normal circumstances airway resistance is about [latex]\text{0.5 to 2.5 cmH}_2\text{O}[/latex].
When we view the airways as a series of tubes, including the trachea, bronchi, and smaller airways, airway resistance can be defined as the constant factor that relates pressure to the flow of air.
[latex]R=\frac{\Delta P}{\Delta\dot V}[/latex]
Key Takeaway
Relate airway resistance back to definitions of pressures. To determine airway resistance, transairway pressure ([latex]P_{TA}[/latex]) will be considered. To determine respiratory system resistance, transrespiratory pressure will be considered.
It is worth noting that the pressure needed to produce airflow during lung inflation accounts for the entirety of airway resistance, even though resistance may fluctuate depending on the specific level of the bronchial tree being examined. Although the right and left main bronchi vary in size, the same driving pressure is transmitted through both of them based on the combined resistance, even tough different flow through these airways created different resistance. Large airways are considered connected in parallel, with the total resistance of elements being less than the resistance of each elements considered individually. Smaller airways are connected in series with large airways as they progress though the bronchial tree. Resistance through the smaller airways will require different pressures for the same flow. The total resistance through smaller airways connected in series is higher than the resistance of an individual element.
Air flow through the conducting airways encounters different patterns: laminar and turbulent flow, and often a combination of these two. Laminar flow requires less pressure to move flow than turbulent flow. Poiseuille's Law describes the factors affecting resistance during laminar flow.
Poiseuille’s Law
Poiseuille’s Law is written as: [latex]\dot V=\frac{\Pi\Delta PR}{8nl}[/latex]
Where:
[latex]\dot V=\text{flow rate}[/latex]
[latex]\Delta P=\text{driving pressure}[/latex]
[latex]R=\text{radius of tube}[/latex]
[latex]\Pi=\text{mathematical constant}[/latex]
[latex]n=\text{viscosity of the fluid}[/latex]
[latex]l=\text{length of the conducting tube}[/latex]
This video offers a summary of the impact of compliance and resistance on breathing.
Time Constants
A time constant represents the time required for the lungs to fill and empty by [latex]63\%[/latex]. Filling of the lungs depends on the driving pressure required based on compliance and resistance. Therefore, a time constant is calculated as the product of compliance and resistance.
This concept is important because it can help us understand differences in distribution of ventilation throughout the lungs, especially in the presence of disease process. Different alveoli, even if adjacent, may have different time constants (different compliance and/or resistance), leading to potentially different driving pressures and volumes. Under normal physiological conditions, a time constant is 0.1 to 0.2 sec.
When inspiratory flow is constant, alveoli with decreased compliance (stiff lung) will have a shorter time constant, will fill quickly, and possibly with smaller volume. These alveoli will require more pressure to deliver normal volume. An example of this scenario is a patient with pulmonary fibrosis.
| [latex]TC=C\times R[/latex] | |
|---|---|
| [latex]1\;TC[/latex] | [latex]63\%[/latex] filling or emptying |
| [latex]2\;TC[/latex] | [latex]86\%[/latex] filling or emptying |
| [latex]3\;TC[/latex] | [latex]95\%[/latex] filling or emptying |
| [latex]4\;TC[/latex] | [latex]98\%[/latex] filling or emptying |
| [latex]5\;TC[/latex] | lung unit fills or empties completely [latex](99.3\%)[/latex] |
Alveoli with high resistance will have a long time constant and will fill more slowly. An example of this scenario is a patient with emphysema. If flow stops long enough at the end of inspiration, air will move from the alveoli with decreased compliance into alveoli with high resistance. This movement of air between alveoli is described as The Pendelluft effect.