9.2 Parallax and the Parsec

Distance within the Solar System

The work of Copernicus and Kepler established the relative distances of the planets—that is, how far from the Sun one planet is compared to another. But their work could not establish the absolute distances (in light-seconds or metres or other standard units of length). This is like knowing the height of all the students in your class only as compared to the height of your astronomy instructor, but not in inches or centimetres. Somebody’s height has to be measured directly.

Similarly, to establish absolute distances, astronomers had to measure one distance in the solar system directly. Generally, the closer to us the object is, the easier such a measurement would be. Estimates of the distance to Venus were made as Venus crossed the face of the Sun in 1761 and 1769, and an international campaign was organized to estimate the distance to the asteroid Eros in the early 1930s, when its orbit brought it close to Earth. More recently, Venus crossed (or transited) the surface of the Sun in 2004 and 2012, and allowed us to make a modern distance estimate, although, as we will see below, by then it wasn’t needed. This transit is pictured in Figure 9.1.

Venus Transits the Sun, 2012

The Transit of Venus in 2012. The solid black disk of Venus is visible just inside the limb of the Sun near the 2 o’clock position in this ultraviolet image taken with the Solar Dynamics Observatory spacecraft.
Figure 9.1. This striking “picture” of Venus crossing the face of the Sun (it’s the black dot at about 2 o’clock) is more than just an impressive image. Taken with the Solar Dynamics Observatory spacecraft and special filters, it shows a modern transit of Venus. Such events allowed astronomers in the 1800s to estimate the distance to Venus. They measured the time it took Venus to cross the face of the Sun from different latitudes on Earth. The differences in times can be used to estimate the distance to the planet. Today, radar is used for much more precise distance estimates.
SDO’s Ultra-high Definition View of 2012 Venus Transit – 171 Angstrom by NASA/SDO, AIA, NASA Media License.

The key to our modern determination of solar system dimensions is radar, a type of radio wave that can bounce off solid objects. A radar is pictured in Figure 9.2. As discussed in several earlier chapters, by timing how long a radar beam (travelling at the speed of light) takes to reach another world and return, we can measure the distance involved very accurately. In 1961, radar signals were bounced off Venus for the first time, providing a direct measurement of the distance from Earth to Venus in terms of light-seconds (from the roundtrip travel time of the radar signal).

Subsequently, radar has been used to determine the distances to Mercury, Mars, the satellites of Jupiter, the rings of Saturn, and several asteroids. Note, by the way, that it is not possible to use radar to measure the distance to the Sun directly because the Sun does not reflect radar very efficiently. But we can measure the distance to many other solar system objects and use Kepler’s laws to give us the distance to the Sun.

Radar Telescope

This is a photograph of one of NASA’s Deep Space Network radio telescopes, seen in profile and pointing skyward.
Figure 9.2. This dish-shaped antenna, part of the NASA Deep Space Network in California’s Mojave Desert, is 70 metres wide. Nicknamed the “Mars antenna,” this radar telescope can send and receive radar waves, and thus measure the distances to planets, satellites, and asteroids. Image by NASA/JPL-Caltech, NASA Media License.

From the various (related) solar system distances, astronomers selected the average distance from Earth to the Sun as our standard “measuring stick” within the solar system. When Earth and the Sun are closest, they are about 147.1 million kilometres apart; when Earth and the Sun are farthest, they are about 152.1 million kilometres apart. The average of these two distances is called the astronomical unit (AU). We then express all the other distances in the solar system in terms of the AU. Years of painstaking analyses of radar measurements have led to a determination of the length of the AU to a precision of about one part in a billion. The length of 1 AU can be expressed in light travel time as 499.004854 light-seconds, or about 8.3 light-minutes. If we use the definition of the meter given previously, this is equivalent to 1 AU = 149,597,870,700 metres.

These distances are, of course, given here to a much higher level of precision than is normally needed. In this text, we are usually content to express numbers to a couple of significant places and leave it at that. For our purposes, it will be sufficient to round off these numbers:

 

[latex]\begin{array}{l} \text{speed of light:}\;c=3\times10^8\text{m/s}=3\times10^5\phantom{\rule{0.2em}{0ex}}\text{km/s} \\ \text{length of light-second: ls}=3\times10^8\text{m}=3\times10^5\text{km} \\ \text{astronomical unit: AU}=1.50\times10^{11}\text{m}=1.50\times10^8\text{km}=500\text{ light-seconds} \end{array}[/latex]

We now know the absolute distance scale within our own solar system with fantastic accuracy. This is the first link in the chain of cosmic distances.

It is an enormous step to go from the planets to the stars. For example, our Voyager 1 probe, which was launched in 1977, has now traveled farther from Earth than any other spacecraft. As of July 2023, Voyager 1 is 160 AU from the Sun. The nearest star, however, is hundreds of thousands of AU from Earth. Even so, we can, in principle, survey distances to the stars using the same technique that a civil engineer employs to survey the distance to an inaccessible mountain or tree—the method of triangulation.

Triangulation in Space

A practical example of triangulation is your own depth perception. As you are pleased to discover every morning when you look in the mirror, your two eyes are located some distance apart. You therefore view the world from two different vantage points, and it is this dual perspective that allows you to get a general sense of how far away objects are.

To see what we mean, take a pen and hold it a few inches in front of your face. Look at it first with one eye (closing the other) and then switch eyes. Note how the pen seems to shift relative to objects across the room. Now hold the pen at arm’s length: the shift is less. If you play with moving the pen for a while, you will notice that the farther away you hold it, the less it seems to shift. Your brain automatically performs such comparisons and gives you a pretty good sense of how far away things in your immediate neighbourhood are.

If your arms were made of rubber, you could stretch the pen far enough away from your eyes that the shift would become imperceptible. This is because our depth perception fails for objects more than a few tens of metres away. In order to see the shift of an object a city block or more from you, your eyes would need to be spread apart a lot farther.

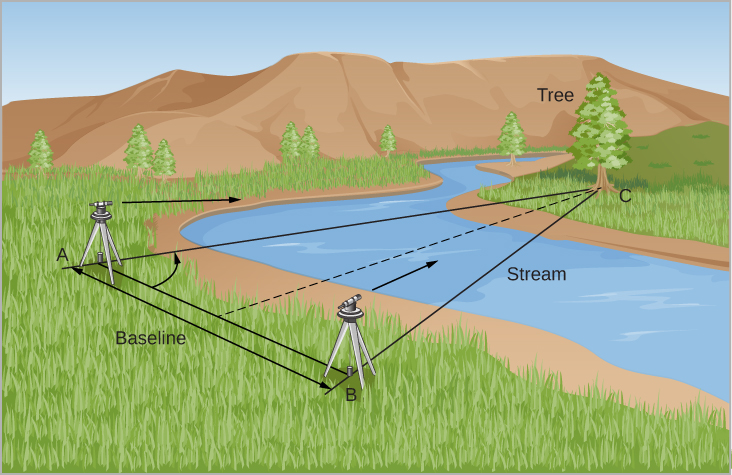
Let’s see how surveyors take advantage of the same idea. Suppose you are trying to measure the distance to a tree across a deep river as shown in Figure 9.3. You set up two observing stations some distance apart. That distance (line AB) is called the baseline. Now the direction to the tree (C in the figure) in relation to the baseline is observed from each station. Note that C appears in different directions from the two stations. This apparent change in direction of the remote object due to a change in vantage point of the observer is called parallax.

Triangulation

Illustration of the Triangulation Method. In this illustration a surveyor’s transit is shown at two positions along a stream of water. Position “A” is at the center left of this image, and position “B” is just below the center of the illustration. They are separated by a distance labelled “Baseline,” with a black line drawn connecting the two. Both instruments are being used to measure the distance to a tree on the far side of the stream which is located at the upper right corner in the illustration. The tree is labelled “C.” Black lines are drawn from positions “A” and “B” to the tree at “C” to create the triangle ABC. A dashed line is drawn from the center of the baseline to point “C.” A curved arrow is drawn from the baseline to the line AC to represent the angle between the baseline and line AC.
Figure 9.3. Triangulation allows us to measure distances to inaccessible objects. By getting the angle to a tree from two different vantage points, we can calculate the properties of the triangle they make and thus the distance to the tree.

The parallax is also the angle that lines AC and BC make—in mathematical terms, the angle subtended by the baseline. A knowledge of the angles at A and B and the length of the baseline, AB, allows the triangle ABC to be solved for any of its dimensions—say, the distance AC or BC. The solution could be reached by constructing a scale drawing or by using trigonometry to make a numerical calculation. If the tree were farther away, the whole triangle would be longer and skinnier, and the parallax angle would be smaller. Thus, we have the general rule that the smaller the parallax, the more distant the object we are measuring must be.

In practice, the kinds of baselines surveyors use for measuring distances on Earth are completely useless when we try to gauge distances in space. The farther away an astronomical object lies, the longer the baseline has to be to give us a reasonable chance of making a measurement. Unfortunately, nearly all astronomical objects are very far away. To measure their distances requires a very large baseline and highly precise angular measurements. The Moon is the only object near enough that its distance can be found fairly accurately with measurements made without a telescope. Ptolemy determined the distance to the Moon correctly to within a few percent. He used the turning Earth itself as a baseline, measuring the position of the Moon relative to the stars at two different times of night.

With the aid of telescopes, later astronomers were able to measure the distances to the nearer planets and asteroids using Earth’s diameter as a baseline. This is how the AU was first established. To reach for the stars, however, requires a much longer baseline for triangulation and extremely sensitive measurements. Such a baseline is provided by Earth’s annual trip around the Sun.

As Earth travels from one side of its orbit to the other, it graciously provides us with a baseline of 2 AU, or about 300 million kilometres. Although this is a much bigger baseline than the diameter of Earth, the stars are so far away that the resulting parallax shift is still not visible to the naked eye—not even for the closest stars.

The first successful detections of stellar parallax were in the year 1838, when Friedrich Bessel in Germany, pictured in Figure 9.4, Thomas Henderson, a Scottish astronomer working at the Cape of Good Hope, and Friedrich Struve in Russia independently measured the parallaxes of the stars 61 Cygni, Alpha Centauri, and Vega, respectively. Even the closest star, Alpha Centauri, showed a total displacement of only about 1.5 arcseconds during the course of a year.

Friedrich Wilhelm Bessel (1784–1846), Thomas J. Henderson (1798–1844), and Friedrich Struve (1793–1864).

Portraits of (a) Friedrich Wilhelm Bessel, (b) Thomas Henderson, and (c) Friedrich Struve.
Figure 9.4. (a) Bessel made the first authenticated measurement of the distance to a star (61 Cygni) in 1838, a feat that had eluded many dedicated astronomers for almost a century. But two others, (b) Scottish astronomer Thomas J. Henderson and (c) Friedrich Struve, in Russia, were close on his heels.

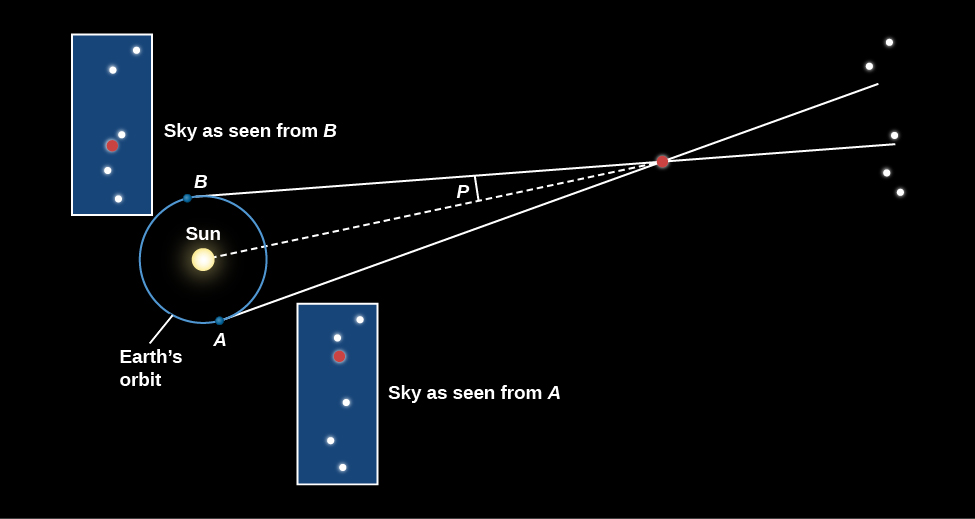
Figure 9.5 shows how such measurements work. Seen from opposite sides of Earth’s orbit, a nearby star shifts position when compared to a pattern of more distant stars. Astronomers actually define parallax to be one-half the angle that a star shifts when seen from opposite sides of Earth’s orbit (the angle labelled P in Figure 9.5). The reason for this definition is just that they prefer to deal with a baseline of 1 AU instead of 2 AU.

Parallax

Illustration of Parallax. The Sun is drawn as a yellow disk in the left hand portion of the diagram and is labelled “Sun.” A blue circle surrounds the Sun and is labelled “Earth’s orbit.” The Earth is shown at two positions on the blue circle. Position “A” at the bottom of the circle and “B” at the top. Above and to the right of the center, a nearby star is drawn as an unlabelled red dot. In the upper right is an unlabelled group of five stars that are more distant than the red star. A white line is drawn from position A through the red dot to the uppermost stars in the group. A white line is drawn from position B through the red dot to the middle star in the group. A dashed line is drawn from the Sun to the red dot. The parallax angle, “p,” is drawn between the dashed line and line B. To illustrate the effect of parallax, two insets are included near points A and B. The inset at point B is labelled “Sky as seen from B,” and shows the red dot near the middle star of the group of five stars that are illustrated in the upper right side of the figure. The inset at point A is labelled “Sky as seen from A,” and shows the red dot near the uppermost stars of the group of five stars that are illustrated in the upper right side of the figure.
Figure 9.5. As Earth revolves around the Sun, the direction in which we see a nearby star varies with respect to distant stars. We define the parallax of the nearby star to be one half of the total change in direction, and we usually measure it in arcseconds.

With a baseline of one AU, how far away would a star have to be to have a parallax of 1 arcsecond? The answer turns out to be 206,265 AU, or 3.26 light-years. This is equal to 3.1 × 1013 kilometres (in other words, 31 trillion kilometres). We give this unit a special name, the parsec (pc)—derived from “the distance at which we have a parallax of one second.” The distance (D) of a star in parsecs is just the reciprocal of its parallax (p) in arcseconds; that is,

[latex]\begin{align*}D=\frac{1}{p}\end{align*}[/latex]

Thus, a star with a parallax of 0.1 arcsecond would be found at a distance of 10 parsecs, and one with a parallax of 0.05 arcsecond would be 20 parsecs away.

Back in the days when most of our distances came from parallax measurements, a parsec was a useful unit of distance, but it is not as intuitive as the light-year. One advantage of the light-year as a unit is that it emphasizes the fact that, as we look out into space, we are also looking back into time. The light that we see from a star 100 light-years away left that star 100 years ago. What we study is not the star as it is now, but rather as it was in the past. The light that reaches our telescopes today from distant galaxies left them before Earth even existed.

In this text, we will use light-years as our unit of distance, but many astronomers still use parsecs when they write technical papers or talk with each other at meetings. To convert between the two distance units, just bear in mind: 1 parsec = 3.26 light-year, and 1 light-year = 0.31 parsec.

Example 9.1

How Far Is a Light-Year?

A light-year is the distance light travels in 1 year. Given that light travels at a speed of 300,000 km/s, how many kilometres are there in a light-year?

Solution

We learned earlier that speed = distance/time. We can rearrange this equation so that distance = velocity × time. Now, we need to determine the number of seconds in a year.

There are approximately 365 days in 1 year. To determine the number of seconds, we must estimate the number of seconds in 1 day.

We can change units as follows (notice how the units of time cancel out):

[latex]\begin{align*}1\phantom{\rule{0.2em}{0ex}}\text{day}\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}24\phantom{\rule{0.2em}{0ex}}\text{hr/day}\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}60\phantom{\rule{0.2em}{0ex}}\text{min/hr}\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}60\phantom{\rule{0.2em}{0ex}}\text{s/min}=86,400\phantom{\rule{0.2em}{0ex}}\text{s/day}\end{align*}[/latex]

Next, to get the number of seconds per year:

[latex]\begin{align*}365\phantom{\rule{0.2em}{0ex}}\text{days/year}\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}86,400\phantom{\rule{0.2em}{0ex}}\text{s/day}=31,536,000\phantom{\rule{0.2em}{0ex}}\text{s/year}\end{align*}[/latex]

Now we can multiply the speed of light by the number of seconds per year to get the distance traveled by light in 1 year:

[latex]\begin{array}{cc}\hfill \text{distance}& =\text{velocity}\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}\text{time}\hfill \\ & =300,000\phantom{\rule{0.2em}{0ex}}\text{km/s}\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}31,536,000\phantom{\rule{0.2em}{0ex}}\text{s}\hfill \\ & =9.46\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}{10}^{12}\phantom{\rule{0.2em}{0ex}}\text{km}\hfill \end{array}[/latex]

That’s almost 10,000,000,000,000 km that light covers in a year. To help you imagine how long this distance is, we’ll mention that a string 1 light-year long could fit around the circumference of Earth 236 million times.

Exercise 9.1

The solution for Example 9.1 is a really large number. What happens if we put it in terms that might be a little more understandable, like the diameter of Earth? Earth’s diameter is about 12,700 km.

Solution

[latex]\begin{array}{cc}\hfill 1\phantom{\rule{0.2em}{0ex}}\text{light-year}& =9.46\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}{10}^{12}\phantom{\rule{0.2em}{0ex}}\text{km}\hfill \\ & =9.46\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}{10}^{12}\phantom{\rule{0.2em}{0ex}}\text{km}\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}\frac{1\phantom{\rule{0.2em}{0ex}}\text{Earth diameter}}{12,700\phantom{\rule{0.2em}{0ex}}\text{km}}\hfill \\ & =7.45\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{Earth diametres}\hfill \end{array}[/latex]

That means that 1 light-year is about 745 million times the diameter of Earth.

Attribution

“19.1 Fundamental Units of Distance” and “19.2 Surveying the Stars” from Douglas College Astronomy 1105 by Douglas College Department of Physics and Astronomy, is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted. Adapted from Astronomy 2e.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Fanshawe College Astronomy Copyright © 2023 by Dr. Iftekhar Haque is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.