"

2.8 Ratios

Ratios and proportions are used in a wide variety of situations to make comparisons. For example, using the information from Figure 2.2, we can see that the number of Facebook users compared to the number of Twitter users is 2,498 m to 386 m. Note that the “m” stands for million, so 2,498 million is actually 2,498,000,000 and 386 million is 386,000,000. Similarly, the number of Qzone users compared to the number of Pinterest users is in a ratio of 517 million to 366 million. These types of comparisons are ratios.

 

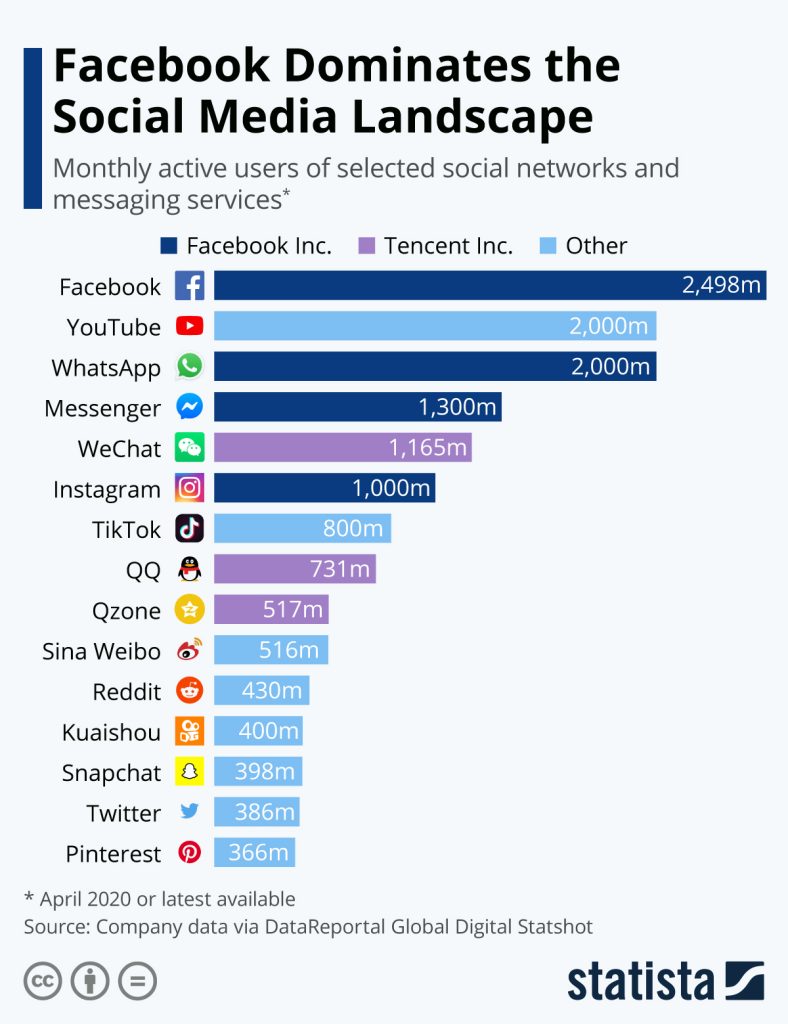
Chart: Facebook Inc. Dominates the Social Media Landscape
Figure 2.2 This bar graph shows popular social media app usage.
Chart: Facebook Inc. Dominates the Social Media Landscape by Statista, CC BY-ND 3.0.

Constructing Ratios to Express Comparison of Two Quantities

Note there are three different ways to write a ratio, which is a comparison of two numbers that can be written as: [latex]a[/latex] to [latex]b[/latex] OR [latex]a:b[/latex] OR the fraction [latex]a/b[/latex]. Which method you use often depends upon the situation. For the most part, we will want to write our ratios using the fraction notation. Note that, while all ratios are fractions, not all fractions are ratios. Ratios make part to part, part to whole, and whole to part comparisons. Fractions make part to whole comparisons only.

Example 2.3

Expressing the Relationship between Two Currencies as a Ratio

The Euro (€) is the most common currency used in Europe. Twenty-two nations, including Italy, France, Germany, Spain, Portugal, and the Netherlands use it. On June 9, 2021, [latex]1[/latex] U.S. dollar was worth [latex]0.82[/latex] Euros. Write this comparison as a ratio.

Solution

Using the definition of ratio, let [latex]a=1[/latex] U.S. dollar and let [latex]b=0.82[/latex] Euros. Then the ratio can be written as either [latex]1[/latex] to [latex]0.82[/latex]; or [latex]1:0.82[/latex]; or [latex]\frac{1}{0.82}[/latex].

Exercise 2.3

On June 9, 2021, [latex]1[/latex] U.S. dollar was worth [latex]1.21[/latex] Canadian dollars. Write this comparison as a ratio.
Solution

[latex]a = 1[/latex] U.S. dollar, and [latex]b = 1.21[/latex] Canadian dollars, the ratio is [latex]1[/latex] to [latex]1.21[/latex]; or [latex]1:1.21[/latex]; or [latex]\frac{1}{1.21}[/latex].

Example 2.4

Expressing the Relationship between Two Weights as a Ratio

The gravitational pull on various planetary bodies in our solar system varies. Because weight is the force of gravity acting upon a mass, the weights of objects is different on various planetary bodies than they are on Earth. For example, a person who weighs [latex]200[/latex] pounds on Earth would weigh only [latex]33[/latex] pounds on the moon! Write this comparison as a ratio.

pounds on Earth and let

Solution

Using the definition of ratio, let [latex]a=200[/latex] pounds on Earth and let [latex]b=33[/latex] pounds on the moon. Then the ratio can be written as either [latex]200[/latex] to [latex]33[/latex]; or [latex]200:33[/latex]; or [latex]\frac{200}{33}[/latex].

Exercise 2.4

A person who weighs [latex]170[/latex] pounds on Earth would weigh [latex]64[/latex] pounds on Mars. Write this comparison as a ratio.
Solution

With [latex]a=170[/latex] pounds on Earth, and [latex]b=64[/latex] pounds on Mars, the ratio is [latex]170[/latex] to [latex]64[/latex]; or [latex]170:64[/latex]; or [latex]\frac{170}{64}[/latex].

Using and Applying Proportional Relationships to Solve Problems

Using proportions to solve problems is a very useful method. It is usually used when you know three parts of the proportion, and one part is unknown. Proportions are often solved by setting up like ratios. If [latex]\frac{a}{b}[/latex] and [latex]\frac{c}{d}[/latex] are two ratios such that [latex]\frac{a}{b}=\frac{c}{d}[/latex] then the fractions are said to be proportional. Also, two fractions [latex]\frac{a}{b}[/latex] and [latex]\frac{c}{d}[/latex] are proportional [latex](\frac{a}{b}=\frac{c}{d})[/latex] if and only if [latex]a\times d=b\times c[/latex].

Example 2.5

Solving a Proportion Involving Two Currencies

You are going to take a trip to France. You have [latex]\$520[/latex] U.S. dollars that you wish to convert to Euros. You know that [latex]1[/latex] U.S. dollar is worth [latex]0.82[/latex] Euros. How much money in Euros can you get in exchange for [latex]\$520[/latex]?

be the variable that represents the unknown. Notice that U.S. dollar amounts are in both numerators and Euro amounts are in both denominators.

Solution

Step 1: Set up the two ratios into a proportion; let [latex]x[/latex] be the variable that represents the unknown. Notice that U.S. dollar amounts are in both numerators and Euro amounts are in both denominators.

[latex]\begin{align*}\frac{1}{0.82}=\frac{520}{x}\end{align*}[/latex]

Step 2: Cross multiply, since the ratios [latex]\frac{a}{b}[/latex] and [latex]\frac{c}{d}[/latex] are proportional, then

[latex]\begin{align*}520(0.82)&=1(x)\\426.4&=x\end{align*}[/latex]

You should receive [latex]426.4[/latex] Euros.

Exercise 2.5

After your trip to France, you have [latex]180[/latex] Euros remaining. You wish to convert them back into U.S. dollars. Assuming the exchange rate is the same ([latex]\$1 =0.82\;\text{€}[/latex]), how many dollars should you receive? Round to the nearest cent if necessary.
Solution

[latex]\$219.51[/latex]

Example 2.6

Solving a Proportion Involving Weights on Different Planets

A person who weighs [latex]170[/latex] pounds on Earth would weigh [latex]64[/latex] pounds on Mars. How much would a typical racehorse ([latex]1,000[/latex] pounds) weigh on Mars? Round your answer to the nearest tenth.

Solution

Step 1: Set up the two ratios into a proportion. Notice the Earth weights are both in the numerator and the Mars weights are both in the denominator.

[latex]\begin{align*}\frac{170}{64}=\frac{1,000}{x}\end{align*}[/latex]

Step 2: Cross multiply, and then divide to solve.

[latex]\begin{align*}170x&=1,000(64)\\170x&=64,000\\\frac{170x}{170}&=\frac{64,000}{170}\\x&=376.5\end{align*}[/latex]

So the [latex]1,000[/latex]-pound horse would weigh about [latex]376.5[/latex] pounds on Mars.

Exercise 2.6

A person who weighs [latex]200[/latex] pounds on Earth would weigh only [latex]33[/latex] pounds on the moon. A 2021 Toyota Prius weighs [latex]3,040[/latex] pounds on Earth; how much would it weigh on the moon? Round to the nearest tenth if necessary.
Solution

[latex]501.6[/latex] pounds

Example 2.7

Solving a Proportion Involving Baking

A cookie recipe needs [latex]2\frac{1}{4}[/latex] cups of flour to make [latex]60[/latex] cookies. Jackie is baking cookies for a large fundraiser; she is told she needs to bake [latex]1,020[/latex] cookies! How many cups of flour will she need?

Solution

Attribution

“5.4 Ratios and Proportions” from Douglas College Astronomy 1105 by Douglas College Department of Physics and Astronomy, is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted. Adapted from Astronomy 2e.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Fanshawe College Astronomy Copyright © 2023 by Dr. Iftekhar Haque is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book