11.13 Black Holes
Most stars end their lives as white dwarfs or neutron stars. When a very massive star collapses at the end of its life, however, not even the mutual repulsion between densely packed neutrons can support the core against its own weight. If the remaining mass of the star’s core is more than about three times that of the Sun (MSun), our theories predict that no known force can stop it from collapsing forever! Gravity simply overwhelms all other forces and crushes the core until it occupies an infinitely small volume. A star in which this occurs may become one of the strangest objects ever predicted by theory—a black hole.
Classical Collapse
Let’s begin with a thought experiment. We want to know what speeds are required to escape from the gravitational pull of different objects. A rocket must be launched from the surface of Earth at a very high speed if it is to escape the pull of Earth’s gravity. In fact, any object—rocket, ball, astronomy book—that is thrown into the air with a velocity less than 11 kilometres per second will soon fall back to Earth’s surface. Only those objects launched with a speed greater than this escape velocity can get away from Earth.
The escape velocity from the surface of the Sun is higher yet—618 kilometres per second. Now imagine that we begin to compress the Sun, forcing it to shrink in diameter. Recall that the pull of gravity depends on both the mass that is pulling you and your distance from the centre of gravity of that mass. If the Sun is compressed, its mass will remain the same, but the distance between a point on the Sun’s surface and the centre will get smaller and smaller. Thus, as we compress the star, the pull of gravity for an object on the shrinking surface will get stronger and stronger as depicted in Figure 11.31.
Formation of a Black Hole
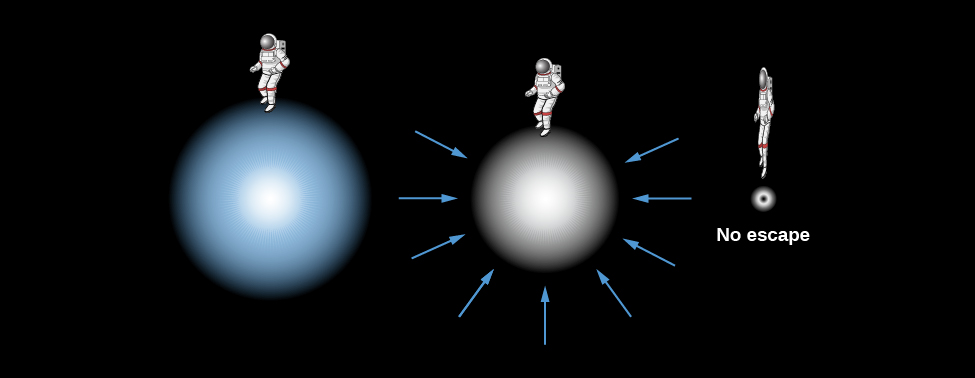
When the shrinking Sun reaches the diameter of a neutron star (about 20 kilometres), the velocity required to escape its gravitational pull will be about half the speed of light. Suppose we continue to compress the Sun to a smaller and smaller diameter. (We saw this can’t happen to a star like our Sun in the real world because of electron degeneracy, i.e., the mutual repulsion between tightly packed electrons; this is just a quick “thought experiment” to get our bearings).
Ultimately, as the Sun shrinks, the escape velocity near the surface would exceed the speed of light. If the speed you need to get away is faster than the fastest possible speed in the universe, then nothing, not even light, is able to escape. An object with such large escape velocity emits no light, and anything that falls into it can never return.
In modern terminology, we call an object from which light cannot escape a black hole, a name popularized by the America scientist John Wheeler starting in the late 1960s, pictured in Figure 11.32. The idea that such objects might exist is, however, not a new one. Cambridge professor and amateur astronomer John Michell wrote a paper in 1783 about the possibility that stars with escape velocities exceeding that of light might exist. And in 1796, the French mathematician Pierre-Simon, marquis de Laplace, made similar calculations using Newton’s theory of gravity; he called the resulting objects “dark bodies.”
John Wheeler (1911–2008)

John Archibald Wheeler by Ulli Steltzer, courtesy of AIP Emilio Segrè Visual Archives, Public Domain.
While these early calculations provided strong hints that something strange should be expected if very massive objects collapse under their own gravity, we really need general relativity theory to give an adequate description of what happens in such a situation.
Collapse with Relativity
General relativity tells us that gravity is really a curvature of spacetime. As gravity increases (as in the collapsing Sun of our thought experiment), the curvature gets larger and larger. Eventually, if the Sun could shrink down to a diameter of about 6 kilometres, only light beams sent out perpendicular to the surface would escape. All others would fall back onto the star as shown in Figure 11.33. If the Sun could then shrink just a little more, even that one remaining light beam would no longer be able to escape.
Light Paths near a Massive Object

Keep in mind that gravity is not pulling on the light. The concentration of matter has curved spacetime, and light (like the trained ant of our earlier example) is “doing its best” to go in a straight line, yet is now confronted with a world in which straight lines that used to go outward have become curved paths that lead back in. The collapsing star is a black hole in this view, because the very concept of “out” has no geometrical meaning. The star has become trapped in its own little pocket of spacetime, from which there is no escape.
The star’s geometry cuts off communication with the rest of the universe at precisely the moment when, in our earlier picture, the escape velocity becomes equal to the speed of light. The size of the star at this moment defines a surface that we call the event horizon. It’s a wonderfully descriptive name: just as objects that sink below our horizon cannot be seen on Earth, so anything happening inside the event horizon can no longer interact with the rest of the universe.
Imagine a future spacecraft foolish enough to land on the surface of a massive star just as it begins to collapse in the way we have been describing. Perhaps the captain is asleep at the gravity meter, and before the crew can say “Albert Einstein,” they have collapsed with the star inside the event horizon. Frantically, they send an escape pod straight outward. But paths outward twist around to become paths inward, and the pod turns around and falls toward the centre of the black hole. They send a radio message to their loved ones, bidding good-bye. But radio waves, like light, must travel through spacetime, and curved spacetime allows nothing to get out. Their final message remains unheard. Events inside the event horizon can never again affect events outside it.
The characteristics of an event horizon were first worked out by astronomer and mathematician Karl Schwarzschild, pictured in Figure 11.34. A member of the German army in World War I, he died in 1916 of an illness he contracted while doing artillery shell calculations on the Russian front. His paper on the theory of event horizons was among the last things he finished as he was dying; it was the first exact solution to Einstein’s equations of general relativity. The radius of the event horizon is called the Schwarzschild radius in his memory.
The event horizon is the boundary of the black hole; calculations show that it does not get smaller once the whole star has collapsed inside it. It is the region that separates the things trapped inside it from the rest of the universe. Anything coming from the outside is also trapped once it comes inside the event horizon. The horizon’s size turns out to depend only on the mass inside it. If the Sun, with its mass of 1 MSun, were to become a black hole (fortunately, it can’t—this is just a thought experiment), the Schwarzschild radius would be about 3 kilometres; thus, the entire black hole would be about one-third the size of a neutron star of that same mass. Feed the black hole some mass, and the horizon will grow—but not very much. Doubling the mass will make the black hole 6 kilometres in radius, still very tiny on the cosmic scale.
The event horizons of more massive black holes have larger radii. For example, if a globular cluster of 100,000 stars (solar masses) could collapse to a black hole, it would be 300,000 kilometres in radius, a little less than half the radius of the Sun. If the entire Galaxy could collapse to a black hole, it would be only about 1012 kilometres in radius—about a tenth of a light year. Smaller masses have correspondingly smaller horizons: for Earth to become a black hole, it would have to be compressed to a radius of only 1 centimetre—less than the size of a grape. A typical asteroid, if crushed to a small enough size to be a black hole, would have the dimensions of an atomic nucleus.
Example 11.2
The Milky Way’s Black Hole
The size of the event horizon of a black hole depends on the mass of the black hole. The greater the mass, the larger the radius of the event horizon. General relativity calculations show that the formula for the Schwarzschild radius (RS) of the event horizon is
where c is the speed of light, G is the gravitational constant, and M is the mass of the black hole. Note that in this formula, 2, G, and c are all constant; only the mass changes from black hole to black hole.
Astronomers have traced the paths of several stars near the centre of our Galaxy and found that they seem to be orbiting an unseen object—dubbed Sgr A* (pronounced “Sagittarius A-star”)—with a mass of about 4 million solar masses. What is the size of its Schwarzschild radius?
Solution
We can substitute data for G, M, and c (from Table 2.4) directly into the equation:
This distance is about one-fifth of the radius of Mercury’s orbit around the Sun, yet the object contains 4 million solar masses and cannot be seen with our largest telescopes. You can see why astronomers are convinced this object is a black hole.
Exercise 11.2
What would be the size of a black hole that contained only as much mass as a typical pickup truck (about 3000 kg)? (Note that something with so little mass could never actually form a black hole, but it’s interesting to think about the result.)
Solution
Substituting the data into our equation gives
[latex]{R}_{\text{S}}=\frac{2GM}{{c}^{2}}=\frac{2\left(6.67\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}{10}^{-11}\text{N}\cdot{\text{m}}^{2}{\text{/kg}}^{2}\right)\left(3000\phantom{\rule{0.2em}{0ex}}\text{kg}\right)}{{\left(3.00\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{m/s}\right)}^{2}}=1.33\phantom{\rule{0.2em}{0ex}}\times\phantom{\rule{0.2em}{0ex}}{10}^{-23}\phantom{\rule{0.2em}{0ex}}\text{m}[/latex].
For comparison, the size of a proton is usually considered to be about 8 × 10−16 m, which would be about ten million times larger.
A Trip into a Black Hole
The fact that scientists cannot see inside black holes has not kept them from trying to calculate what they are like. One of the first things these calculations showed was that the formation of a black hole obliterates nearly all information about the star that collapsed to form it. Physicists like to say “black holes have no hair,” meaning that nothing sticks out of a black hole to give us clues about what kind of star produced it or what material has fallen inside. The only information a black hole can reveal about itself is its mass, its spin (rotation), and whether it has any electrical charge.
What happens to the collapsing star-core that made the black hole? Our best calculations predict that the material will continue to collapse under its own weight, forming an infinitely squozen point—a place of zero volume and infinite density—to which we give the name singularity. At the singularity, spacetime ceases to exist. The laws of physics as we know them break down. We do not yet have the physical understanding or the mathematical tools to describe the singularity itself, or even if singularities actually occur. From the outside, however, the entire structure of a basic black hole (one that is not rotating) can be described as a singularity surrounded by an event horizon. Compared to humans, black holes are really very simple objects.
Scientists have also calculated what would happen if an astronaut were to fall into a black hole. Let’s take up an observing position a long, safe distance away from the event horizon and watch this astronaut fall toward it. At first he falls away from us, moving ever faster, just as though he were approaching any massive star. However, as he nears the event horizon of the black hole, things change. The strong gravitational field around the black hole will make his clocks run more slowly, when seen from our outside perspective.
If, as he approaches the event horizon, he sends out a signal once per second according to his clock, we will see the spacing between his signals grow longer and longer until it becomes infinitely long when he reaches the event horizon. (Recalling our discussion of gravitational redshift, we could say that if the infalling astronaut uses a blue light to send his signals every second, we will see the light get redder and redder until its wavelength is nearly infinite.) As the spacing between clock ticks approaches infinity, it will appear to us that the astronaut is slowly coming to a stop, frozen in time at the event horizon.
In the same way, all matter falling into a black hole will also appear to an outside observer to stop at the event horizon, frozen in place and taking an infinite time to fall through it. But don’t think that matter falling into a black hole will therefore be easily visible at the event horizon. The tremendous redshift will make it very difficult to observe any radiation from the “frozen” victims of the black hole.
This, however, is only how we, located far away from the black hole, see things. To the astronaut, his time goes at its normal rate and he falls right on through the event horizon into the black hole. (Remember, this horizon is not a physical barrier, but only a region in space where the curvature of spacetime makes escape impossible.)
You may have trouble with the idea that you (watching from far away) and the astronaut (falling in) have such different ideas about what has happened. This is the reason Einstein’s ideas about space and time are called theories of relativity. What each observer measures about the world depends on (is relative to) his or her frame of reference. The observer in strong gravity measures time and space differently from the one sitting in weaker gravity. When Einstein proposed these ideas, many scientists also had difficulty with the idea that two such different views of the same event could be correct, each in its own “world,” and they tried to find a mistake in the calculations. There were no mistakes: we and the astronaut really would see him fall into a black hole very differently.
For the astronaut, there is no turning back. Once inside the event horizon, the astronaut, along with any signals from his radio transmitter, will remain hidden forever from the universe outside. He will, however, not have a long time (from his perspective) to feel sorry for himself as he approaches the black hole. Suppose he is falling feet first. The force of gravity that the singularity exerts on his feet is greater than on his head, so he will be stretched slightly. Because the singularity is a point, the left side of his body will be pulled slightly toward the right, and the right slightly toward the left, bringing each side closer to the singularity. The astronaut will therefore be slightly squeezed in one direction and stretched in the other. Some scientists like to call this process of stretching and narrowing spaghettification. The point at which the astronaut becomes so stretched that he perishes depends on the size of the black hole. For black holes with masses billions of times the mass of the Sun, such as those found at the centres of galaxies, the spaghettification becomes significant only after the astronaut passes through the event horizon. For black holes with masses of a few solar masses, the astronaut will be stretched and ripped apart even before he reaches the event horizon.
Earth exerts similar tidal forces on an astronaut performing a spacewalk. In the case of Earth, the tidal forces are so small that they pose no threat to the health and safety of the astronaut. Not so in the case of a black hole. Sooner or later, as the astronaut approaches the black hole, the tidal forces will become so great that the astronaut will be ripped apart, eventually reduced to a collection of individual atoms that will continue their inexorable fall into the singularity.
Requirements for a Black Hole
So, here is a prescription for finding a black hole: start by looking for a star whose motion (determined from the Doppler shift of its spectral lines) shows it to be a member of a binary star system. If both stars are visible, neither can be a black hole, so focus your attention on just those systems where only one star of the pair is visible, even with our most sensitive telescopes.
Being invisible is not enough, however, because a relatively faint star might be hard to see next to the glare of a brilliant companion or if it is shrouded by dust. And even if the star really is invisible, it could be a neutron star. Therefore, we must also have evidence that the unseen star has a mass too high to be a neutron star and that it is a collapsed object—an extremely small stellar remnant.
We can use Kepler’s law and our knowledge of the visible star to measure the mass of the invisible member of the pair. If the mass is greater than about 3 MSun, then we are likely seeing (or, more precisely, not seeing) a black hole—as long as we can make sure the object really is a collapsed star.
If matter falls toward a compact object of high gravity, the material is accelerated to high speed. Near the event horizon of a black hole, matter is moving at velocities that approach the speed of light. As the atoms whirl chaotically toward the event horizon, they rub against each other; internal friction can heat them to temperatures of 100 million K or more. Such hot matter emits radiation in the form of flickering X-rays. The last part of our prescription, then, is to look for a source of X-rays associated with the binary system. Since X-rays do not penetrate Earth’s atmosphere, such sources must be found using X-ray telescopes in space.
In our example, the infalling gas that produces the X-ray emission comes from the black hole’s companion star. Stars in close binary systems can exchange mass, especially as one of the members expands into a red giant. Suppose that one star in a double-star system has evolved to a black hole and that the second star begins to expand. If the two stars are not too far apart, the outer layers of the expanding star may reach the point where the black hole exerts more gravitational force on them than do the inner layers of the red giant to which the atmosphere belongs. The outer atmosphere then passes through the point of no return between the stars and falls toward the black hole.
The mutual revolution of the giant star and the black hole causes the material falling toward the black hole to spiral around it rather than flow directly into it. The infalling gas whirls around the black hole in a pancake of matter called an accretion disk. It is within the inner part of this disk that matter is revolving about the black hole so fast that internal friction heats it up to X-ray–emitting temperatures (see the image below).
Another way to form an accretion disk in a binary star system is to have a powerful stellar wind come from the black hole’s companion. Such winds are a characteristic of several stages in a star’s life. Some of the ejected gas in the wind will then flow close enough to the black hole to be captured by it into the disk, shown in Figure 11.35.
Binary Black Hole

Modification of image by ESO/L. Calçada, CC BY-4.0.
We should point out that, as often happens, the measurements we have been discussing are not quite as simple as they are described in introductory textbooks. In real life, Kepler’s law allows us to calculate only the combined mass of the two stars in the binary system. We must learn more about the visible star of the pair and its history to ascertain the distance to the binary pair, the true size of the visible star’s orbit, and how the orbit of the two stars is tilted toward Earth, something we can rarely measure. And neutron stars can also have accretion disks that produce X-rays, so astronomers must study the properties of these X-rays carefully when trying to determine what kind of object is at the centre of the disk. Nevertheless, a number of systems that clearly contain black holes have now been found.
Attribution
"24.1 Introducing General Relativity", "24.5 Black Holes", and "24.6 Evidence for Black Holes" from Douglas College Astronomy 1105 by Douglas College Department of Physics and Astronomy, are licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted. Adapted from Astronomy 2e.


