11.10 Type II Supernovae
After the helium in its core is exhausted, the evolution of a massive star takes a significantly different course from that of lower-mass stars. In a massive star, the weight of the outer layers is sufficient to force the carbon core to contract until it becomes hot enough to fuse carbon into oxygen, neon, and magnesium. This cycle of contraction, heating, and the ignition of another nuclear fuel repeats several more times. After each of the possible nuclear fuels is exhausted, the core contracts again until it reaches a new temperature high enough to fuse still-heavier nuclei. The products of carbon fusion can be further converted into silicon, sulphur, calcium, and argon. And these elements, when heated to a still-higher temperature, can combine to produce iron. Massive stars go through these stages very, very quickly. In really massive stars, some fusion stages toward the very end can take only months or even days! This is a far cry from the millions of years they spend in the main-sequence stage.
At this stage of its evolution, a massive star resembles an onion with an iron core. As we get farther from the centre, we find shells of decreasing temperature in which nuclear reactions involve nuclei of progressively lower mass—silicon and sulphur, oxygen, neon, carbon, helium, and finally, hydrogen as shown in Figure 11.21.
Structure of an Old Massive Star
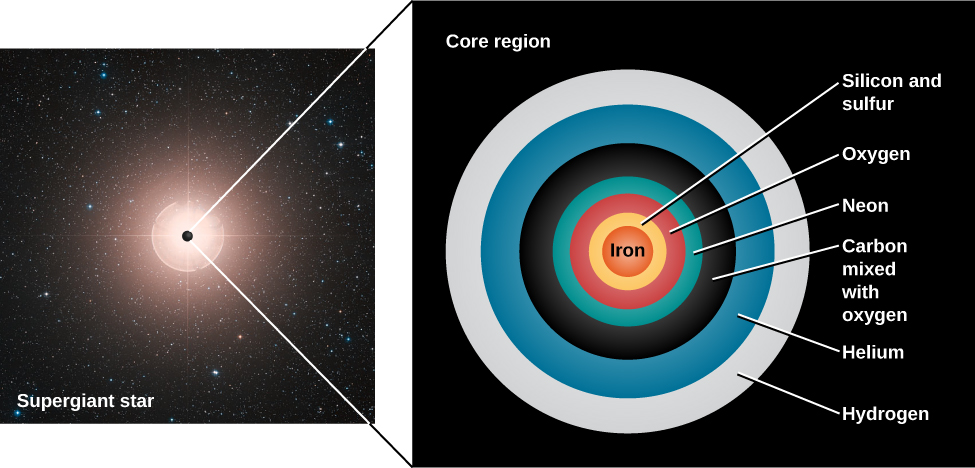
Modification of Digitized Sky Survey image of Betelgeuse by ESO, Digitized Sky Survey, CC-BY-4.0.
But there is a limit to how long this process of building up elements by fusion can go on. The fusion of silicon into iron turns out to be the last step in the sequence of nonexplosive element production. Up to this point, each fusion reaction has produced energy because the nucleus of each fusion product has been a bit more stable than the nuclei that formed it. As discussed before, light nuclei give up some of their binding energy in the process of fusing into more tightly bound, heavier nuclei. It is this released energy that maintains the outward pressure in the core so that the star does not collapse. But of all the nuclei known, iron is the most tightly bound and thus the most stable.
You might think of the situation like this: all smaller nuclei want to “grow up” to be like iron, and they are willing to pay (produce energy) to move toward that goal. But iron is a mature nucleus with good self-esteem, perfectly content being iron; it requires payment (must absorb energy) to change its stable nuclear structure. This is the exact opposite of what has happened in each nuclear reaction so far: instead of providing energy to balance the inward pull of gravity, any nuclear reactions involving iron would remove some energy from the core of the star.
Unable to generate energy, the star now faces catastrophe.
When nuclear reactions stop, the core of a massive star is supported by degenerate electrons, just as a white dwarf is. For stars that begin their evolution with masses of at least 10 MSun, this core is likely made mainly of iron. (For stars with initial masses in the range 8 to 10 MSun, the core is likely made of oxygen, neon, and magnesium, because the star never gets hot enough to form elements as heavy as iron. The exact composition of the cores of stars in this mass range is very difficult to determine because of the complex physical characteristics in the cores, particularly at the very high densities and temperatures involved.) We will focus on the more massive iron cores in our discussion.
While no energy is being generated within the white dwarf core of the star, fusion still occurs in the shells that surround the core. As the shells finish their fusion reactions and stop producing energy, the ashes of the last reaction fall onto the white dwarf core, increasing its mass. As we saw earlier, a higher mass means a smaller core due to the larger gravity pressure. The core can contract because even a degenerate gas is still mostly empty space. Electrons and atomic nuclei are, after all, extremely small. The electrons and nuclei in a stellar core may be crowded compared to the air in your room, but there is still lots of space between them.
The electrons at first resist being crowded closer together, and so the core shrinks only a small amount. Ultimately, however, the iron core reaches a mass so large that even degenerate electrons can no longer support it. When the density reaches 4 × 1011 g/cm3 (400 billion times the density of water), some electrons are actually squeezed into the atomic nuclei, where they combine with protons to form neutrons and neutrinos. This transformation is not something that is familiar from everyday life, but becomes very important as such a massive star core collapses.
Some of the electrons are now gone, so the core can no longer resist the crushing mass of the star’s overlying layers. The core begins to shrink rapidly. More and more electrons are now pushed into the atomic nuclei, which ultimately become so saturated with neutrons that they cannot hold onto them.
At this point, the neutrons are squeezed out of the nuclei and can exert a new force. As is true for electrons, it turns out that the neutrons strongly resist being in the same place and moving in the same way. The force that can be exerted by such degenerate neutrons is much greater than that produced by degenerate electrons, so unless the core is too massive, they can ultimately stop the collapse.
This means the collapsing core can reach a stable state as a crushed ball made mainly of neutrons, which astronomers call a neutron star. We don’t have an exact number (a “Chandrasekhar limit”) for the maximum mass of a neutron star, but calculations tell us that the upper mass limit of a body made of neutrons might only be about 3 MSun. So if the mass of the core were greater than this, then even neutron degeneracy would not be able to stop the core from collapsing further. The dying star must end up as something even more extremely compressed, which until recently was believed to be only one possible type of object—the state of ultimate compaction known as a black hole. This is because no force was believed to exist that could stop a collapse beyond the neutron star stage.
When the collapse of a high-mass star’s core is stopped by degenerate neutrons, the core is saved from further destruction, but it turns out that the rest of the star is literally blown apart. Here’s how it happens.
The collapse that takes place when electrons are absorbed into the nuclei is very rapid. In less than a second, a core with a mass of about 1 MSun, which originally was approximately the size of Earth, collapses to a diameter of less than 20 kilometres. The speed with which material falls inward reaches one-fourth the speed of light. The collapse halts only when the density of the core exceeds the density of an atomic nucleus (which is the densest form of matter we know). A typical neutron star is so compressed that to duplicate its density, we would have to squeeze all the people in the world into a single sugar cube! This would give us one sugar cube’s worth (one cubic centimetre’s worth) of a neutron star.
The neutron degenerate core strongly resists further compression, abruptly halting the collapse. The shock of the sudden jolt initiates a shock wave that starts to propagate outward. However, this shock alone is not enough to create a star explosion. The energy produced by the outflowing matter is quickly absorbed by atomic nuclei in the dense, overlying layers of gas, where it breaks up the nuclei into individual neutrons and protons.
Our understanding of nuclear processes indicates (as we mentioned above) that each time an electron and a proton in the star’s core merge to make a neutron, the merger releases a neutrino. These ghostly subatomic particles carry away some of the nuclear energy. It is their presence that launches the final disastrous explosion of the star. The total energy contained in the neutrinos is huge. In the initial second of the star’s explosion, the power carried by the neutrinos (1046 watts) is greater than the power put out by all the stars in over a billion galaxies.
While neutrinos ordinarily do not interact very much with ordinary matter (we earlier accused them of being downright antisocial), matter near the center of a collapsing star is so dense that the neutrinos do interact with it to some degree. They deposit some of this energy in the layers of the star just outside the core. This huge, sudden input of energy reverses the infall of these layers and drives them explosively outward. Most of the mass of the star (apart from that which went into the neutron star in the core) is then ejected outward into space. As we saw earlier, such an explosion requires a star of at least 8 MSun, and the neutron star can have a mass of at most 3 MSun. Consequently, at least five times the mass of our Sun is ejected into space in each such explosive event!
The resulting explosion is called a supernova, it is pictured in Figure 11.22 below. When these explosions happen close by, they can be among the most spectacular celestial events, as we will discuss in the next section.
Five Supernova Explosions in Other Galaxies
Host Galaxies of Distant Supernovae by NASA, ESA, and A. Riess (STScI), NASA Media License.
Table 11.6 summarizes the discussion so far about what happens to stars and substellar objects of different initial masses at the ends of their lives. Like so much of our scientific understanding, this list represents a progress report: it is the best we can do with our present models and observations. The mass limits corresponding to various outcomes may change somewhat as models are improved. There is much we do not yet understand about the details of what happens when stars die.
| Initial Mass (Mass of Sun = 1) | Final State at the End of Its Life |
|---|---|
| <0.01 | Planet |
| 0.01 to 0.08 | Brown dwarf |
| 0.08 to 0.25 | White dwarf made mostly of helium |
| 0.25 to 8 | White dwarf made mostly of carbon and oxygen |
| 8 to 10 | White dwarf made of oxygen, neon, and magnesium |
| 10 to 40 | Supernova explosion that leaves a neutron star |
| > 40 | Supernova explosion that leaves a black hole |
Attribution
“23.2 Evolution of Massive Stars: An Explosive Finish ” from Douglas College Astronomy 1105 by Douglas College Department of Physics and Astronomy, is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted. Adapted from Astronomy 2e.

