Chapter 7: Semantics
7.12 Introduction to set theory
We just introduced denotation as a way of thinking about linguistic meaning. Let’s consider the word cat. The sense of this word would be whatever meaning of cat that you store in your mental lexicon, but the denotation of it would be the set of all cats in the actual world. Terminologically, “things” that are in a set are called members (or elements) of that set. Recall from the previous section that double brackets mean ‘the denotation of (the linguistic expression)’. So, ⟦cat⟧ in (1)should be read as ‘the denotation of the linguistic expression cat‘.
| (1) | ⟦cat⟧ = the set of all cats in the actual world |
Recall also that names denote the individual that the name refers to. So the name Panks, the nickname for my cat, denotes the individual (the cat) named Panks in the actual world (the cat in the foreground in Figure 7.16).
| (2) | ⟦ Panks ⟧ = the individual Panks in the actual world |

Sentences denote the truth value of the sentence, which can also be expressed as a truth condition. When we think about the meaning of intransitive predicates like cat as sets of things, this gives us an intuitive way to characterise the truth condition of a sentence like Panks is a cat. This sentence is true if the individual Panks is among the set of cats in the actual world.
| (3) | ⟦ Panks is a cat ⟧ = T if the individual Panks is a member of the set of all cats in the actual world, F otherwise |
Since Panks indeed is a cat, the sentence in (3) would denote the truth value T. On the other hand, let’s say that Karti is a name of a dog (see Figure 7.17) (4) would be the denotation of the sentence Karti is a cat. It would denote F this time, because Karti is not among the set of cats in our world.
| (4) | ⟦ Karti is a cat ⟧ = T if the individual Karti is a member of the set of all cats in the actual world, F otherwise |

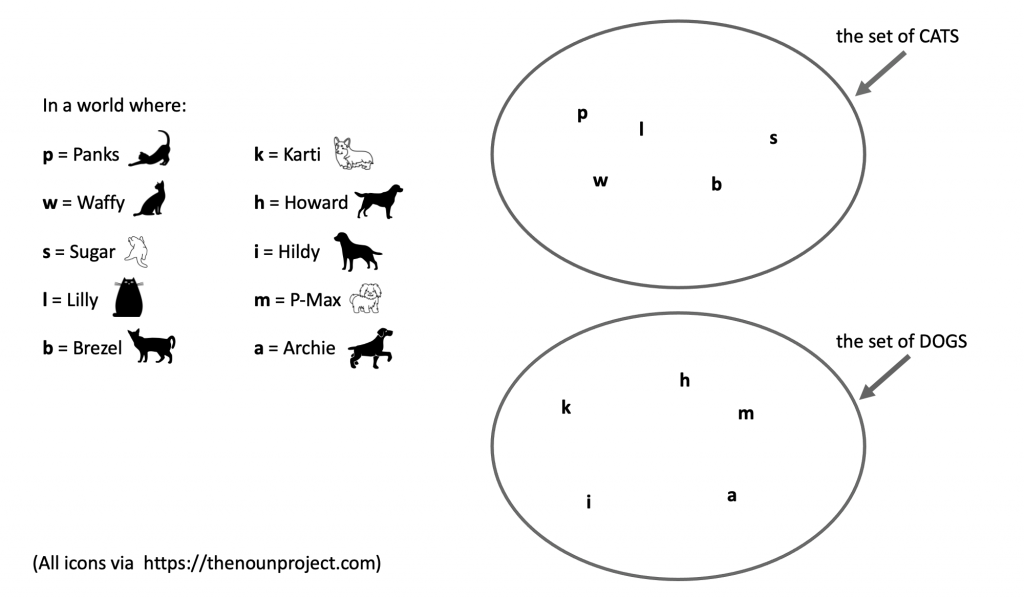
The concept of set membership is illustrated in Figure 7.18. Let’s say we live in a world where the listed animals are the only animals that exist. The top circle represents the set of cats in this world. The bottom circle represents the set of dogs in this world. The sentence Panks is a cat expresses Pank’s set membership relationship in this world: Panks can be found as a member in the top circle. The reason that Karti is a cat is false is because Karti cannot be found in this circle (he can, however, be found in the set of dogs).
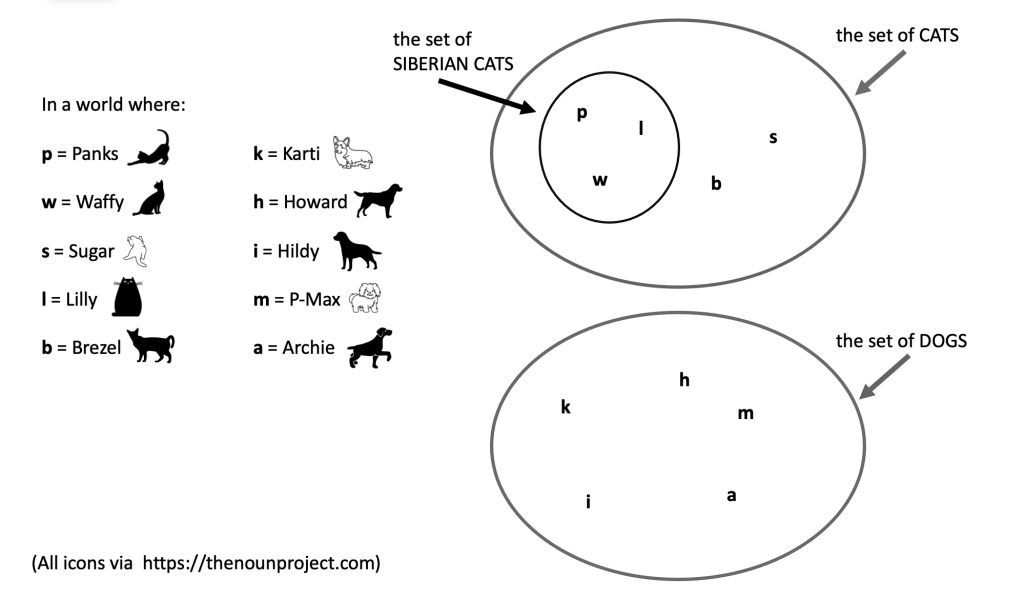
There can be smaller sets within a set. In other words, if we look at the set of cats in Figure 7.19, there could be a subgroup of cats that have a certain property in common. For example, let’s say Panks, Waffy, and Lilly are Siberian Forest Cats (Siberian Cats), and that Sugar and Brezel are not. We can say that the set containing just Panks, Waffy, and Lilly is a subset of the set of cats.
A more formal definition of the subset relation goes like this; let’s use the variables A and B to represent sets (capital letters are usually used for variables and constants that stand for a set).
| (5) | A is a subset of B if all members of A are also members of B. |
As you can see, Panks, Waffy, and Lilly are members of the set of Siberian Cats. Panks, Waffy, and Lilly are also members of the set of cats. Therefore, the set of Siberian Cats is a subset of the set of cats. In logic, the subset symbol is ⊆. A⊆B can be read as ‘A is a subset of B’. So in our example, if we call the set of cats C and the set of Siberian Cats S, the subset relationship can be stated as S⊆C.
In the definition given in (5), we can also say that B is a superset of A. In our example, the set of cats is a superset of the set of Siberian Cats. The superset symbol is simply the subset symbol flipped. So C⊇S reads as ‘C is a superset of S’.
According to the definition in (5), it also means that if A and B contained exactly the same members, A would still be a subset of B and vice versa. If we want to specifically discuss how some members of B are not in A (like how not all cats are Siberian Cats in Figure 7.19), the term proper subset is used. (6) is the formal definition of proper subset.
| (6) | A is a proper subset of B if all members of A are also members of B, and there is at least one member of B which is not a member of A. |
So in Figure 7.19, S is a subset of C, but S is also a proper subset of C. The symbol for proper subset is ⊂: so we can write S⊂C. We can also say that B is a proper superset of A in the definition described in (6). The superset symbol is ⊃, so we can write C⊃S for our example in Figure 7.19.
The symbols that were are using here borrow from a branch of mathematics that studies sets, called set theory. Table 1 below summarises some common set theory notations.
Table 7.1. Set theory notation.
| Notation | Meaning |
| A | The set A. Capital letters are used to refer to sets. |
| { a, b, c } | The set containing members a, b, and c. |
| b ∈ A | b is a member of A. |
| d ∉ A | d is not a member of A. |
| A⊆B | A is a subset of B. |
| B⊇A | B is a superset of A. |
| A⊂B | A is a proper subset of B. |
| B⊃A | B is a proper superset of A. |
| A = B | A is identical to B (that is, A and B have exactly the same members) |
| |A| | The cardinality of A. That is, the number of members in A. |
| |A| = 3 | The cardinality of A is equal to 3. That is, there are three members in A. |
| A∩B | The intersection of A and B. This set contains objects that are both a member of A and a member of B. |
| A∪B | The union of A and B. This set contains objects that are either a member of A or a member of B. |
Set theory is useful for understanding how the meaning of some quantificational words work in language. Quantificational means having to do with quantity, or how much of something. In English, there are quantificational determiners like every, some, most, many, few, two, five, and so on. In order to understand the meaning of a sentence like Two cats are grey let’s think about set intersection. Let’s say there is a set of cats (call it C). Let’s say there’s another set, a set of grey things (call it G). When you take the intersection (or overlap) of C and G, that’s the set of cats that are grey (see Figure 7.20). This can be written as C∩G in set theory notation.
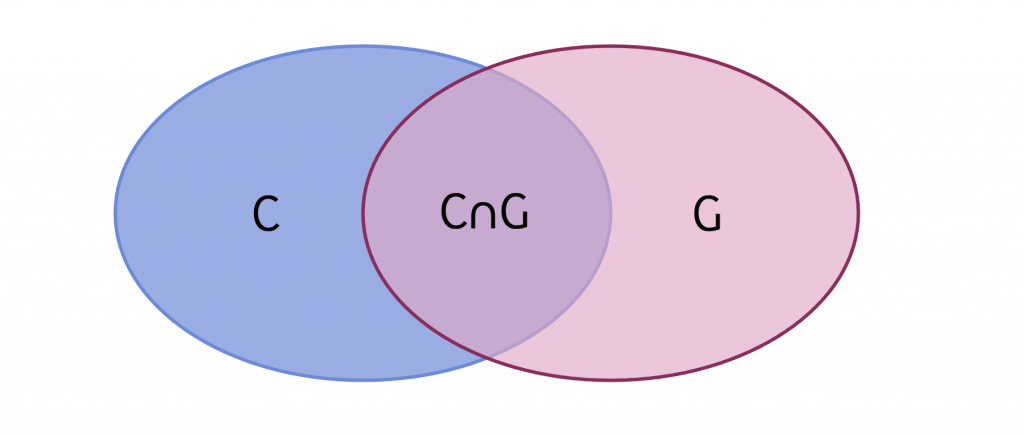
The quantificational determiner two essentially asks the question of, “How many things are in this intersection, C∩G?”. The determiner two says “two things”. Now think about every: What does Every cat is grey mean in terms of sets? It means that all things in the cat set, C, are also in the grey set, G. Formal set theory notation is not super important in this textbook — all you need to retain for the next section is what a superset and a subset is, conceptually. For the advanced learner, try the exercises at the end of this section to see if you can write Panks is a cat, Two cats are grey, and Every cat is grey in set theory notation!
Check your understanding
References
Gamut, L. T. F. (1991). Logic, Language and Meaning Vol. 1. University of Chicago Press.

