7.4 Graphical Solutions to Linear Optimization Problems
Wouldn’t it be nice if we could simply produce and sell infinitely many units of a product and thus make a never-ending amount of money? In business (and in day-to-day living) we know that some things are just unreasonable or impossible. Instead, our hope is to maximize or minimize some quantity, given a set of constraints.
In order to have a linear programming problem, we must have:
- Constraints, represented as inequalities
- An objective function, that is, a function whose value we either want to be as large as possible (want to maximize it) or as small as possible (want to minimize it).
Consider this extension of the example from the end of the last section.
Example 7.4 A
A company produces a basic and premium version of its product. The basic version requires 20 minutes of assembly and 15 minutes of painting. The premium version requires 30 minutes of assembly and 30 minutes of painting. If the company has staffing for 3,900 minutes of assembly and 3,300 minutes of painting each week. They sell the basic products for a profit of $30 and the premium products for a profit of $40. How many of each version should be produced to maximize profit?
Let [latex]b[/latex] = the number of basic products made, and [latex]p[/latex] = the number of premium products made. Our objective function is what we’re trying to maximize or minimize. In this case, we’re trying to maximize profit. The total profit, [latex]P[/latex], is
[latex]P = 30b + 40p[/latex]
In the last section, the example developed our constraints. Together, these define our linear programming problem:
Objective function: [latex]P = 30b + 40p[/latex]
Constraints:
[latex]\begin{align*} 20b + 30p&\leq3900\\ 15b + 30p&\leq3300\\ b&\geq0, p\geq0\\ \end{align*}[/latex]
In this section, we will approach this type of problem graphically. We start by graphing the constraints to determine the feasible region – the set of possible solutions. Just showing the solution set where the four inequalities overlap, we see a clear region.
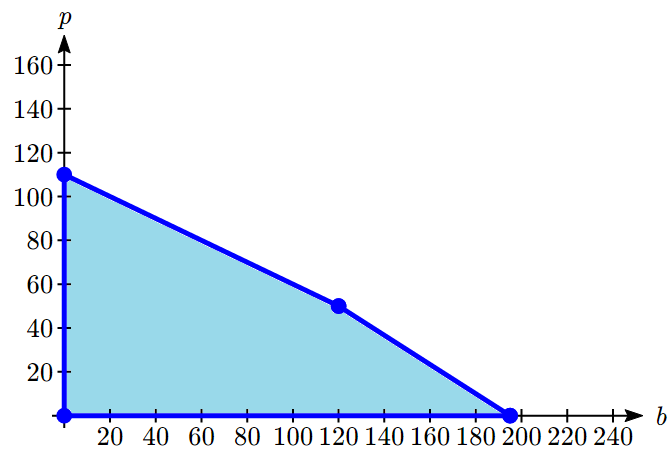
To consider how the objective function connects, suppose we considered all the possible production combinations that gave a profit of [latex]P = $3000[/latex], so that [latex]3000 = 30b + 40p[/latex]. That set of combinations would form a line in the graph. Doing the same for a profit of $5000 and $6500 would give additional lines. Graphing those on top of our feasible region, we see a pattern:
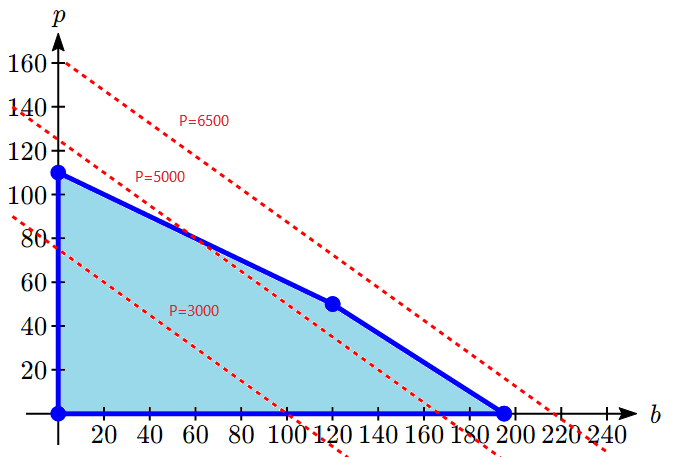
Notice that all the constant-profit lines are parallel, and that in general the profit increases as we move up to upper right. Notice also that for a profit of $5000 there are some production levels inside the feasible region for that profit level, but some are outside. That means we could feasibly make $5000 profit by producing, for example, 167 basic items and no premium items, but we can’t make $5000 by producing 125 premium items and no basic items because that falls outside our constraints.
The solution to our linear programming problem will be the largest possible profit that is still feasible. Graphically, that means the line furthest to the upper-right that still touches the feasible region on at least point. That solution is the one below:
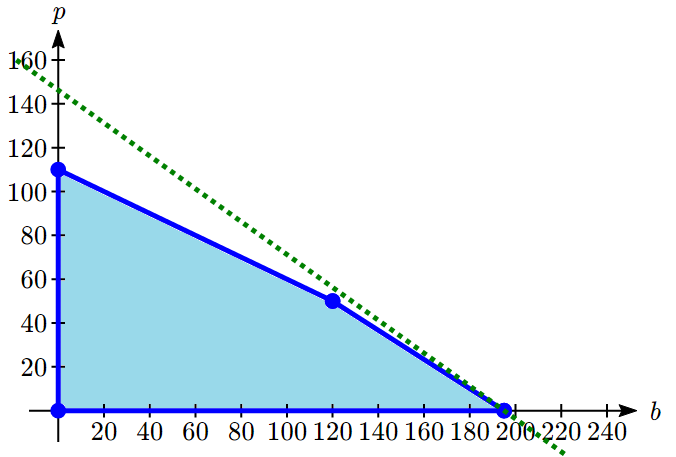
This profit line touches the feasible region where [latex]b = 195[/latex] and [latex]p = 0[/latex], giving a profit of [latex]P[/latex] = 30(195) + 40(0) = $5850.
Notice that this is slightly larger than the profit that would be made by completely utilizing all staffing at [latex]b = 120[/latex], [latex]p = 50[/latex], where the profit would be $5600.
The objective function along with the four corner points above forms a bounded linear programming problem. That is, imagine you are looking at three fence posts connected by fencing (black point and lines, respectively). If you were to put your dog in the middle, you could be sure it would not escape (assuming the fence is tall enough). If this is the case, then you have a bounded linear programming problem. If the dog could walk infinitely in any one direction, then the problem is unbounded.
In the past example, you can see that the line of maximum profit will always touch the boundary of the feasible region. That observation inspires the fundamental theorem of linear programming.
Fundamental Theorem of Linear Programming
- If a solution exists to a bounded linear programming problem, then it occurs at one of the corner points.
- If a feasible region is unbounded, then a maximum value for the objective function does not exist.
- If a feasible region is unbounded, and the objective function has only positive coefficients, then a minimum value exists.
In the last example we solve the problem somewhat intuitively by “sliding” the profit line up. Typically we use a more procedural approach.
Solving a Linear Programming Problem Graphically
- Define the variables to be optimized. The question asked is a good indicator as to what these will be.
- Write the objective function, first in words, then convert to a mathematical equation
- Write the constraints, first in words, then convert to mathematical inequalities
- Graph the constraints inequalities, and shade the feasible region
- Identify the corner points by solving systems of linear equations whose intersection represents a corner point.
- Test all corner points in the objective function. The “winning” point is the point that optimizes the objective function (biggest if maximizing, smallest if minimizing)
Give It Some Thought
1. Maximize [latex]P = 14x + 9y[/latex] subject to the constraints:
[latex]\begin{align*} x + y &\leq 9\\ 3x + y &\leq 15\\ x &\geq 0 , y \geq 0\\ \end{align*}[/latex]
Example 7.4 B
A health-food business would like to create a high-potassium blend of dried fruit in the form of a box of 10 fruit bars. It decides to use dried apricots, which have 407 mg of potassium per serving, and dried dates, which have 271 mg of potassium per serving. The company can purchase its fruit in bulk for a reasonable price. Dried apricots cost $9.99/lb. (about 3 servings) and dried dates cost $7.99/lb. (about 4 servings). The company would like the box of bars to have at least the recommended daily potassium intake of about 4700 mg, and contain at least 1 serving of each fruit. In order to minimize cost, how many servings of each dried fruit should go into the box of bars?
We begin by defining the variables. Let
[latex]x[/latex] = number of servings of dried apricots
[latex]y[/latex] = number of servings of dried dates
We next work on the objective function.
For apricots, there are 3 servings in one pound. This means that the cost per serving is $9.99/3 = $3.33. The cost for [latex]x[/latex] servings would thus be [latex]3.33x[/latex].
For dates, there are 4 servings per pound. This means that the cost per serving is $7.99/4 = $2.00. The cost for [latex]y[/latex] servings would thus be [latex]2.00y[/latex].
The total cost, [latex]C[/latex], for apricots and dates would be [latex]C = 3.33x + 2.00y[/latex]
Normally we would have constraints [latex]x\geq0[/latex] and [latex]y\geq0[/latex] since negative servings can’t be used. But in this case, we’re further restricted. In words:
- There must be at least 1 serving of each fruit
- The product must contain at least 4700 mg of potassium
Mathematically,
- Since there must be at least 1 serving of each fruit, [latex]x\geq1[/latex] and [latex]y\geq1[/latex]
- There are [latex]407x[/latex] mg of potassium in [latex]x[/latex] servings of apricots and [latex]271y[/latex] mg of potassium in [latex]y[/latex] servings of dates. The sum should be greater than or equal to 4700 mg of potassium, or [latex]407x + 271y\geq4700[/latex]
Thus we have,
Objective function:
[latex]C = 3.33x + 2.00y[/latex]
Constraints:
[latex]\begin{align*} 407x + 271y&\geq4700\\ x&\geq1 , y\geq1 \end{align*}[/latex]
We graph the constraints and shade the feasible region:
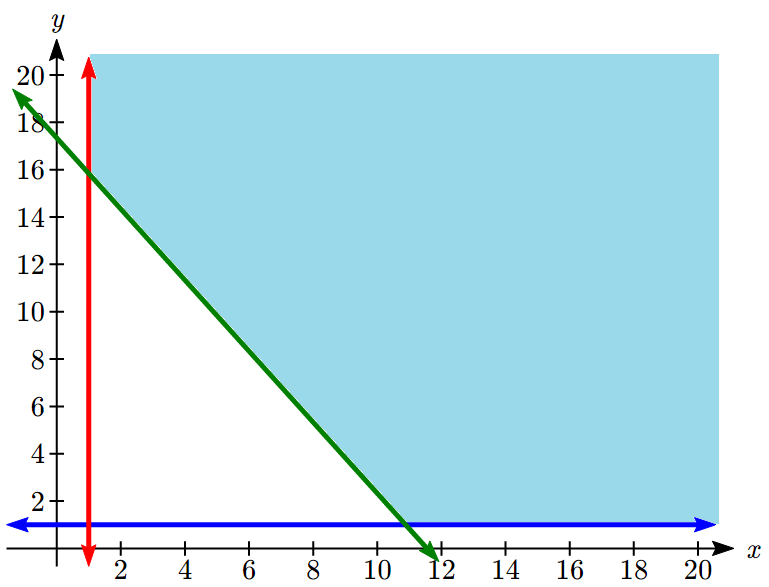
The region is unbounded, but we will be able to find a minimum still. We can see there are two corner points.
The one in the upper left is the intersection of the lines [latex]407x + 271y = 4700[/latex] and [latex]x = 1[/latex]. Solving for the intersection using substitution:
\begin{align*}
407(1) + 271y &= 4700\\
y &\approx 15.8\\
\end{align*}
Point: [latex](1, 15.8)[/latex]
The one in the lower right is the intersection of the lines [latex]407x + 271y = 4700[/latex] and [latex]y = 1[/latex].
\begin{align*}
407x + 271(1) &= 4700\\
x &\approx 10.9\\
\end{align*}
Point: [latex](10.9, 1)[/latex]
Testing the objective function at each of these corner points:
| Point | Cost, [latex]C = 3.33x + 2.00y[/latex] |
| [latex](10.9, 1)[/latex] | [latex]C = 3.33(10.9) + 2.00(1)= \$38.30[/latex] |
| [latex](1, 15.8)[/latex] | [latex]C = 3.33(1) + 2.00(15.8) = \$34.96[/latex] |
The company can minimize cost by using 1 serving of apricots and 15.8 servings of dates.
Give It Some Thought
2. A company makes two products. Product A requires 3 hours of manufacturing and 1 hour of assembly. Product B requires 4 hours of manufacturing and 2 hours of assembly. There are a total of 84 hours of manufacturing and 32 hours of assembly available. Determine the production to maximize profit if the profit on product A is $50 and the profit on product B is $60.
Example 7.4 C
A factory manufactures chairs and tables, each requiring the use of three operations: Cutting, Assembly, and Finishing. The first operation can be used at most 40 hours; the second at most 42 hours; and the third at most 25 hours. A chair requires 1 hour of cutting, 2 hours of assembly, and 1 hour of finishing; a table needs 2 hours of cutting, 1 hour of assembly, and 1 hour of finishing. If the profit is $20 per unit for a chair and $30 for a table, how many units of each should be manufactured to maximize profit?
We begin by defining the variables. Let
[latex]c[/latex] = number of chairs made
[latex]t[/latex] = number of tables made
The profit, [latex]P[/latex], will be [latex]P = 20c + 30t[/latex].
For cutting, [latex]c[/latex] chairs will require [latex]1c[/latex] hours and [latex]t[/latex] tables will require [latex]2t[/latex] hours. We can use at most 40 hours, so [latex]c + 2t \leq40[/latex].
For assembly, [latex]c[/latex] chairs will require [latex]2c[/latex] hours and [latex]t[/latex] tables will require [latex]1t[/latex] hours. We can use at most 42 hours, so [latex]2c + t\leq42[/latex].
For finishing, [latex]c[/latex] chairs will require [latex]1c[/latex] hours and [latex]t[/latex] tables will require [latex]1t[/latex] hours. We can use at most 25 hours, so [latex]c + t\leq25[/latex].
Since we can’t produce negative items, [latex]c\geq 0, t \geq 0[/latex].
Graphing the constraints, we can see the feasible region.
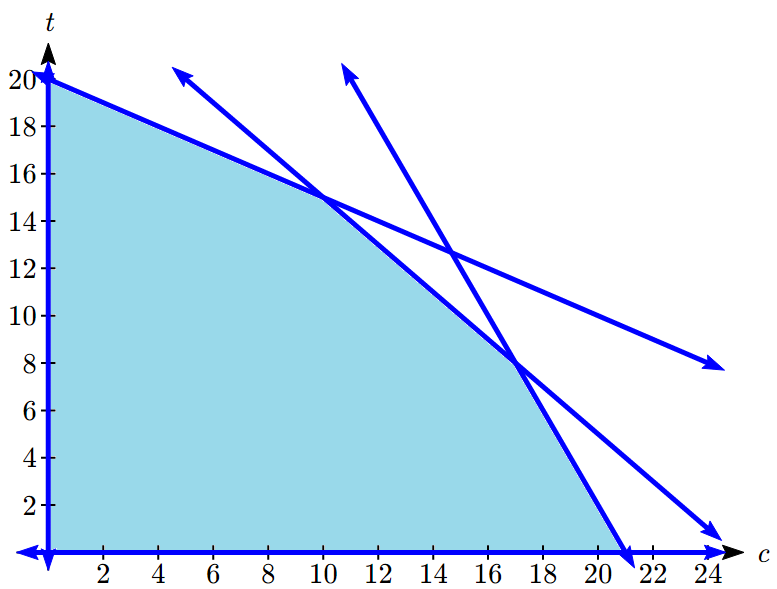
There are five corner points for this region.
Point 1: In the lower left, where [latex]t = 0[/latex] crosses [latex]c = 0[/latex].
Point: [latex](0, 0)[/latex]
Point 2: In the upper left, where [latex]c = 0[/latex] crosses [latex]c + 2t = 40[/latex].
Using substitution, [latex]0 + 2t = 40[/latex], so [latex]t = 20[/latex].
Point: [latex](0, 20)[/latex]
Point 3: In the lower right, where [latex]t = 0[/latex] crosses [latex]2c + t = 42[/latex].
Using substitution, [latex]2c + 0 = 42[/latex], so [latex]c = 21[/latex].
Point: [latex](21, 0)[/latex]
Point 4: Where [latex]c + 2t = 40[/latex] crosses [latex]2c + t = 42[/latex].
We can solve this as a system using any techniques we know. We could solve the second equation for [latex]c[/latex], giving [latex]c = 25 - t[/latex], then substitute into the first equation:
[latex]\begin{align*} (25 - t) + 2t &= 40\\ 25 + t &= 40\\ t &= 15\\ \end{align*}[/latex]
Then [latex]c = 25 – 15 = 10[/latex].
Point: [latex](10, 15)[/latex]
Point 5: Where [latex]2c + t = 42[/latex] crosses [latex]c + t = 25[/latex].
We can solve this as a system using any techniques we know. Using a different technique this time, we could multiply the bottom equation by -1 then add it to the first:
[latex]\begin{align*} 2c + t &= 42\\ -c - t &= -25 & {\textrm{equation 1- equation 2}}\\ c &= 17\\ \end{align*}[/latex]
Then using [latex]c + t = 25[/latex], we have [latex]17 + t = 25[/latex], so [latex]t = 8[/latex].
Point: [latex](17, 8)[/latex]
Testing the objective function at each of these corner points:
| Point | Profit, [latex]P = 20c + 30t[/latex] |
| [latex](0, 0)[/latex] | [latex]P = 20(0) + 30(0) = \$0[/latex] |
| [latex](0, 20)[/latex] | [latex]P = 20(0) + 30(20) = \$600[/latex] |
| [latex](21, 0)[/latex] | [latex]P = 20(21) + 30(0) = \$420[/latex] |
| [latex](10, 15)[/latex] | [latex]P = 20(10) + 30(15) = \$650[/latex] |
| [latex](17, 8)[/latex] | [latex]P = 20(17) + 30(8) = \$580[/latex] |
The profit will be maximized by producing 10 chairs and 15 tables.
Give It Some Thought Answers
- Maximize [latex]P=14x+9y[/latex] subject to:
[latex]\begin{align*} x + y &\leq 9\\ 3x + y &\leq 15\\ x &\geq 0,y \geq 0 \end{align*}[/latex]
Graphing the feasible region, we see there are three corner points of potential interest: [latex](0, 9)[/latex], [latex](5, 0)[/latex], and the intersection of the two lines at [latex](3, 6)[/latex]. We then evaluate the objective function at each corner point.
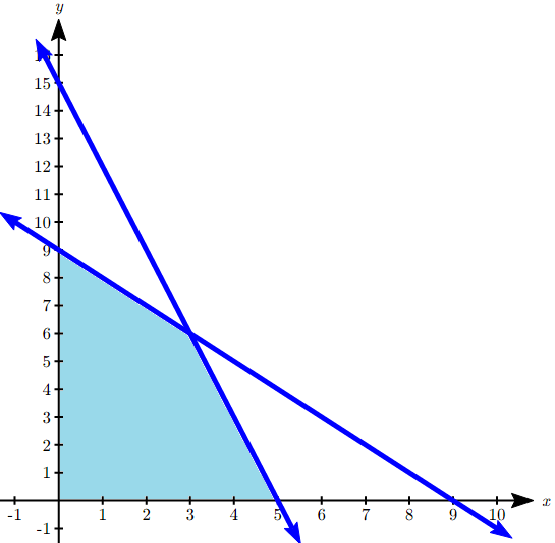
| Point | [latex]P=14x+9y[/latex] |
| [latex](0, 9)[/latex] | 81 |
| [latex]5, 0)[/latex] | 70 |
[latex]P[/latex] is maximized when [latex]x = 3[/latex], [latex]y = 6[/latex].
- Let [latex]a[/latex] be the number of product A produced, and [latex]b[/latex] be the number of product B.
Our goal is to maximize profit: [latex]P = 50a + 60b[/latex].
From manufacturing we get the constraint:
[latex]3a + 4b \leq 84[/latex]
From assembly we get the constraint:
[latex]1a + 2b \leq 32[/latex]
We have corner points at (0, 16), (28, 0). The third is at the intersection of the two lines. To find that we could multiply the second equation by -2 and add:
[latex]\begin{align*} 3a+4b&=84\\ -2a-4b&=-64 & \text{equation 1- equation 2}\\ a&=20\\ \end{align*}[/latex]
The third corner point is at [latex](20, 6)[/latex].

Evaluating the objective function at each of these points:
| Point | [latex]P[/latex] |
| [latex](0, 16[/latex] | [latex]P=50(0)+60(16)=960[/latex] |
Profit will be maximized by producing 28 units of product A and 0 units of product B.
Section Exercises
Work on section 7.4 exercises in Fundamentals of Business Math Exercises. Discuss your solutions with your peers and/or course instructor.
You may consult answers to select exercises: Fundamentals of Business Math Exercises – Select Answers

