5.3 Exchange Rates and Currency Exchange
Section Exercises – after the reading
Work on section 5.3 exercises in Fundamentals of Business Math Exercises after reading this section. Discuss your solutions with your peers and/or course instructor.
You may consult answers to select exercises: Fundamentals of Business Math Exercises – Select Answers
You have set aside $6,000 in Canadian funds toward hostel costs during a long backpacking trip through the United States, Mexico, and Europe. After searching on the Internet, you decide to use airbnb.com to reserve your hostel rooms. The website quotes you the following amounts for each country: 1,980 US dollars, 21,675 Mexican pesos, and 1,400 euros. Have you allocated enough money to cover these costs?
Whether you are a consumer backpacking around the world on distant vacations, investing in international securities, or shopping online at global Internet sites, you must pay for your purchases in local currencies out of your Canadian currency accounts. Businesses are no different as they export and import products to and from other countries. With outsourcing on the rise, it is also common for business services such as call centres and advertising agencies to be located abroad along with manufacturing facilities. Large-scale companies may have operations in several countries throughout the world.
All of these transactions and operations require the conversion of Canadian currency to a foreign currency or vice versa. This section shows you the basics of currency conversion rates. It then explores finer details such as charges for currency conversion and what happens when one currency gets stronger or weaker relative to another.
Exchange Rates
An exchange rate between two currencies is defined as the number of units of a foreign currency that are bought with one unit of the domestic currency, or vice versa. Since two currencies are involved in every transaction, two published exchange rates are available. Let’s use Canada and the United States to illustrate this concept.
- The first exchange rate indicates what one dollar of Canada’s currency becomes in US currency.
- The second exchange rate indicates what one dollar of US currency becomes in Canadian currency.
These two exchange rates allow Canadians to determine how many US dollars their money can buy and vice versa. These currency rates have an inverse relationship to one another: if 1 Canadian dollar equals 0.80 US dollars, then 1 US dollar equals = 1.25 Canadian dollars. The best way to view currency exchange rates is through proportions.
Most Canadian daily and business newspapers publish exchange rates in their financial sections. Although exchange rates are published in a variety of ways, a currency cross-rate table, like the table below, is most common. Note that exchange rates fluctuate all of the time as currencies are actively traded in exchange markets. Therefore, any published table needs to indicate the date and time at which the rates were determined. Also note that the cells where the same currency appears show no published rate as you never need to convert from Canadian dollars to Canadian dollars!
| C$ | US$ | € | ¥ | MXN$ | AU$ | |
| Canadian Dollar (C$) | —— | 1.2648 | 1.4667 | 0.0114 | 0.0618 | 0.918 |
| US Dollar (US$) | 0.7906 | —— | 1.1596 | 0.009 | 0.0489 | 0.7258 |
| Euro (€) | 0.6818 | 0.8624 | —— | 0.0078 | 0.0422 | 0.6259 |
| Japanese Yen (¥) | 87.8004 | 111.05 | 128.7736 | —— | 0.184 | 80.6001 |
| Mexican Peso (MXN$) | 16.1812 | 20.4487 | 23.7123 | 5.4348 | —— | 14.8565 |
| Australian Dollar (AU$) | 1.0893 | 1.3778 | 1.5977 | 0.0124 | 0.0673 | —— |
In the table, all exchange rates have been rounded to four decimals. In true exchange markets, most exchange rates are expressed in 10 decimals or more such that currency exchanges in larger denominations are precisely performed. For the purposes of this textbook, we will use a four decimal standard to simplify the calculations while still illustrating the principles of currency exchange.
Also note that it is not stated in this table whether it is columns or the rows that represent the currency being converted or the currency being converted to. Typically this information is displayed in notes associated in the table. You must verify which is which before using the data from the table.
In this table, the columns represent the currency we are converting from, and the row represent the currency we are converting to. This is a typical set up in cross rates tables but make sure that you verify, rather than assume. It may also be helpful to think of the columns as “per”. For example, the row for Japanese yen and the column for Canadian dollars represents the amount of yen per one Canadian dollar.
So the information in the table above says, for example, that
[latex]87.8004:1=\text{amount in ¥ }:\text{amount in C\$}[/latex]
This also means that one Canadian dollar is worth 87.8004 Japanese yen.
Technically, only half of the table is needed, since one side of the diagonal line is nothing more than the inverse of the other. For example, one C$ is equal to 0.6818 euros, as shown on the bottom of the diagonal. The inverse, or [latex]\frac{1}{{0.7137}}= 1.4667[/latex] is the value of one euro in Canadian dollars and is what is listed on top of the diagonal.
The Fundamental Currency Exchange Relationship
Follow the ratio [latex]\text{new currency}:\text{original currency}[/latex] and set up the proportion accordingly, then solve for the unknown value:
[latex]\text{exchange rate}_{orig \to new}:{1}={\text{new currency amt}}:{\text{original currency amt}}[/latex]
This can be rewritten as
[latex]\text{new currency amt}=({\text{exchange rate}}_{orig \to new})({\text{original currency amt}})[/latex]
Currencies, exchange rates, and currency cross-tables all raise issues regarding decimals and financial fees.
- Decimals in Currencies. Not all currencies in the world have decimals. Here in North America, MXN$, US$, and C$ have two decimals. Mexicans call those decimals centavos while Canadians and Americans call them cents. Australia and the European countries using the euro also have cents. However, the Japanese yen does not have any decimals in its currency. If you are unsure about the usage of decimals, perform a quick Internet search to clarify the issue.
- Financial Fees. Technically, the rates in a cross-rate table are known as mid-rates. A mid-rate is an exchange rate that does not involve or provide for any charges for currency conversion. When you convert currencies, you need to involve a financial organization, which will charge for its services.
- Sell Rates. When you go to a bank and convert your domestic money to a foreign currency, the bank charges you a sell rate, which is the rate at which a foreign currency is sold. When you exchange your money, think of this much like a purchase at a store—the bank’s product is the foreign currency and the price it charges is marked up to its selling price. The sell rate is always higher than the mid-rate in terms of C$ per unit of foreign currency and thus is always lower than the mid-rate in terms of foreign currency per unit of C$. For example, the exchange rate of US$ to C$ is 1.2468. This means it will cost you C$1.2468 to purchase US$1.00. The bank, though, will sell you this money for a sell rate that is higher, say $1.2470. This means it will cost you an extra C$0.02 per US$ to exchange the money. That $0.02 difference is the fee from the bank for its services, and it is how the bank makes a profit on the transaction.
- Buy Rates. When you go to a bank and convert your foreign currency back into your domestic money, the bank charges you a buy rate, which is the rate at which a foreign currency is purchased. The buy rate is always lower than the mid-rate in terms of C$ per unit of foreign currency and thus is always higher than the mid-rate in terms of foreign currency per unit of C$. Using the same example as above, if you want to take your US$1.00 to the bank and convert it back to Canadian funds, the bank charges you a buy rate that is lower, say $0.7904. In other words, you receive C$0.02 less per US$. Again, the $0.02 difference is the bank’s fee for making the currency exchange on your behalf.
How It Works
This section opened with your backpacking vacation to the United States, Mexico, and Europe, for which you were quoted prices of US$1,980, MXN$21,675, and €1,400 for hostels. Assume all purchases are made with your credit card and that your credit card company charges 2.5% on all currency exchanges. Can your C$6,000 budget cover these costs?
Can the budget cover the cost? We need total cost of purchases.
Canadian to US: [latex]1:0.7906=\text{amount in C\$}:\text{amount in US\$}[/latex]
[latex]\begin{align*} \Rightarrow \text{amount in US\$}&=0.7906(\text{amount in C\$})\\ \Rightarrow (\text{amount in C\$})&=\frac{ \text{amount in US\$}}{0.7906}\\ &=\frac{ 1980}{0.7906}\\ &=C\$ 2,504.43\\ \end{align*}[/latex]
Canadian to Mexican: [latex]1:16.1812=\text{amount in C\$}:\text{amount in MXN\$}[/latex]
[latex]\begin{align*} \Rightarrow \text{amount in MXN\$}&=16.1812(\text{amount in C\$})\\\\ \Rightarrow (\text{amount in C\$})&=\frac{ \text{amount in MXN\$}}{16.1812}\\\\ &=\frac{ 21675}{16.1812}\\\\ &=C\$ 1,339.52\\\\ \end{align*}[/latex]
Canadian to euros: [latex]1:16.1812=\text{amount in C\$}:\text{amount in €}[/latex]
[latex]\begin{align*} \Rightarrow \text{amount in €}&=0.6818(\text{amount in C\$})\\\\ \Rightarrow (\text{amount in C\$})&=\frac{ \text{amount in €}}{0.6818}\\\\ &=\frac{ 1400}{0.6818}\\\\ &=C\$ 2,053.39 \\\\ \end{align*}[/latex]
Putting the three amounts together, together with the 2.5% credit card charge on exchange, your total hostel bill is:
[latex](1+0.025)(2504.43 + 1339.52 + 2053.39) = \$6,044.77[/latex]
Because this is over budget by C$44.77, you will have to adjust your vacation plans.
Note: Instead of going Canadian dollars to other currency, we could have gone other currency to Canadian dollars. In that case we would have used the inverse values from the cross rates table and our ratios would be different. Try it out!
Things To Watch Out For
When working with currency exchange, probably the trickiest element is that you have to choose one of two inverse exchange rates depending on which way the money conversion is taking place. In any currency situation, it is important that you take the time to understand the basis on which the currency rate is being expressed. Typically, exchange rates are expressed on a per-unit basis in the country’s domestic currency. For example, Canadians express the US dollar exchange rate on a per C$ basis. From the cross-rate table, that exchange rate is 1.0218. In contrast, Americans express the Canadian dollar exchange rate on a per US$ basis, or 0.9787.
Paths To Success
Let the buyer beware when it comes to international transactions. If you have ever purchased and returned an item to an international seller, you may have noticed that you did not receive all of your money back. For most consumers, international purchases are made via credit cards. What most consumers do not know is that the credit card companies do in fact use buy and sell rates that typically charge 2.5% of the exchange rate when both buying and selling.
For example, if you purchase a US$2,000 item at the rates listed in the cross-rate table, your credit card is charged $2,000 × 0.9787(1.025) = $2,006.40. If you return an item you do not want, your credit card is refunded $2,000 × 0.9787(0.975) = $1,908.40. In other words, you are out $2,006.40 − $1,908.40 = $98! This amount represents your credit card company’s charge for the currency conversion—a whopping 4.9% of your purchase price!
Give It Some Thought
- In each of the following situations and using the cross-rate table, determine on a strictly numerical basis whether you would have more or fewer units of the target currency than of the original currency. You want to convert:
- C$ into US$
- AU$ into MXN$
- MXN$ into ¥
- C$ into €
Example 5.3 A: Straight Currency Conversion
Strictly using the mid-rates from the cross-rate table presented earlier, if you wanted to convert C$1,500 into MXN$ for your spring break vacation in Cancun, Mexico, how many Mexican pesos would you have?
Answer: amount in Mexican pesos?
Canadian to Mexican: [latex]1:16.1812=\text{amount in C\$}:\text{amount in MXN\$}[/latex]
[latex]\begin{align*} \Rightarrow \text{amount in MXN\$}&=16.1812(\text{amount in C\$})\\\\ &={16.1812}\cdot 1500\\\\ &=\text{MXN\$ } 24,271.80\\\\ \end{align*}[/latex]
Example 5.3 B: Calculating Profit Using Buy and Sell Rates
A Mexican manufacturer imports its parts from Canada and assembles its product in Mexico, then exports some of the finished product back to Canada to sell at retail. Suppose the total cost of the imported parts, purchased and paid for in Canadian funds, is C$5.50 per unit, assembly costs are MXN$24.54 per unit, and expenses are MXN$4.38 per unit. If the product is exported back to Canada at a selling price of C$9.95 (for which its Canadian customers pay in Canadian funds), what is the total profit in Mexican pesos on 10,000 units? The manufacturer’s financial institution charges a sell rate 2% higher than the mid-rate and has a buy rate that is 3% lower than the mid-rate. Use the mid-rates from the cross-rate table.
Answer: total profit in Mexican pesos on 10,000 units?
[latex]\text{profit in MXN\$} = \text{revenue in MXN\$}- \text{cost in MXN\$}[/latex]
Since [latex]{\text{new currency amount}}=({\text{exchange rate}}_{orig \to new})({\text{original currency amt}})[/latex]
we have [latex]\text{amount in MXN\$}=(\text{exchange rate}_{C\to MXN}) (\text{amount in C\$})[/latex]
Sell rate from MXN$ to C$: 2% on mid-rate = (1+0.02)(mid-rate)
Buy rate from C$ to MXN$: 3% on mid-rate = (1-0.03)(mid-rate)
Let’s consider the revenue. Here the Canadian currency revenues are reduced by the financial institution’s conversion fee, so buy rate is applied.
[latex]\begin{align*} \text{revenue in MXN\$} &= (\text{selling price in MXN\$})(\text{number of units})\\\\ &=(\text{buy rate})(\text{selling price in C\$})(\text{number of units})\\\\ &=(1-0.03)(16.1812)(9.95)(10000)\\\\ &=\text{MXN\$ } 1,561,728.52 \end{align*}[/latex]
Let’s consider the cost. Here the Canadian currency costs are increased by the financial institution’s conversion fee, so sell rate is applied.
[latex]\begin{align*} \text{cost in MXN\$} &=(\text{import unit cost in MXN\$}+\text{assembly unit cost in MXN\$}+ \text{unit expenses in MXN\$})(\text{# units})\\\\ &=(\text{sell rate})(\text{selling price in C\$}+\text{assembly unit cost in MXN\$}+\text{unit expenses in MXN\$})(\text{# units})\\\\ &=((1+0.02)(16.1812)(5.50)+24.54+4.38)(10000)\\\\ &=\text{MXN\$ } 1,196,965.32 \end{align*}[/latex]
Therefore, the total profit is
[latex]\begin{align*} \text{profit in MXN\$} &= \text{revenue in MXN\$}- \text{cost in MXN\$}\\\\ &=1,561,728.52-1,196,965.32\\\\ &=\text{MXN\$ }364,763.20 \end{align*}[/latex]
Currency Appreciation and Depreciation
An analyst on Global News is discussing how the Canadian dollar has strengthened against the US dollar. Your first reaction is that a strong Canadian dollar ought to be good thing, so hearing that this change might hurt Canada’s exports, you wonder how that could be.
Currencies are actively traded in the international marketplace, which means that exchange rates are changing all the time. As such, exchange rates rise and decline. A currency appreciates (or strengthens) relative to another currency when it is able to purchase more of that other currency than it could previously. A currency depreciates (or weakens) relative to another currency when it is able to purchase less of that other currency than it could previously. Take a look at two examples illustrating these concepts:
- EXAMPLE 1: If C$1 buys US$1.02 and the exchange rate rises to US$1.03, then your C$1 purchases an additional penny of the US dollars. Therefore, the Canadian currency appreciates, or strengthens, relative to the US dollar.
- EXAMPLE 2: Similarly, if the exchange rate drops to US$1.01, then your C$1 purchases one less penny of the US dollars. Therefore, the Canadian currency depreciates, or weakens, relative to the US dollar.
These concepts are particularly important to international business and global economies. Generally speaking, when a currency appreciates, it has a positive effect on imports from the other country because it costs less money than it used to for domestic companies to purchase the same amount of products from the other country. However, the currency appreciation tends to also have a negative effect on exports to other countries because it costs the foreign companies more money to purchase the same amount of products from the domestic companies.
Important Notes
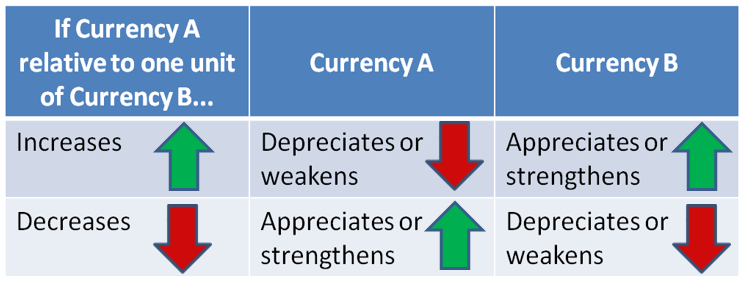
It is critical to observe that if currency A appreciates relative to currency B, then the opposite is true for currency B relative to currency A (currency B depreciates relative to currency A). The figure to the right illustrates this concept. Recalling Example 1 above, the Canadian currency appreciated, so the US currency depreciated. In Example 2, the Canadian currency depreciated, so the US currency appreciated.
How It Works
When you work with currency appreciation or depreciation, you still use the same basic steps as before. The additional skill you require in the first step is to adjust an exchange rate appropriately based on how it has appreciated or depreciated.
Things To Watch Out For
It is very easy to confuse the two relative currencies, their values, and the concepts of appreciation and depreciation. For example, if the exchange rate increases between currency A relative to a unit of currency B, which exchange rate appreciated? If currency A has increased per unit of currency B, then it takes more money of currency A to buy one unit of currency B. As a result, currency B appreciates because a single unit of currency B can now buy more of currency A. For example, if the exchange rate is US$1.0218 relative to C$1 and it increases to US$1.0318 relative to C$1, then the Canadian dollar purchases one penny more. The figure helps you understand the relationships involved and provides a visual reminder of which direction everything is moving.
Give It Some Thought
- Consider the relationship in relative change between currencies in relation to their appreciation and depreciation in the following examples.
- If the exchange rate in terms of US dollars per unit of euros increases, which currency weakened?
- If the Australian dollar weakens against the Canadian dollar, did the exchange rate increase or decrease in terms of Australian dollars per unit of Canadian dollars?
- If the exchange rate in terms of yen per unit of the Mexican pesos decreases, which currency weakened?
- If the British pound (£) appreciates against the US dollar, did the exchange rate increase or decrease in terms of pounds per unit of US dollars?
Example 5.3 C: Effect of Currency Appreciation
A Canadian manufacturer requires parts from the United States. It purchases from its supplier in lots of 100,000 units at a price of US$7.25 per unit. Since the last time the manufacturer made a purchase, the Canadian dollar has appreciated 0.0178 from the previous mid-rate of US$1.0218 per C$. If the sell rate is 1.5% above the mid-rate, how have the manufacturer’s costs changed?
Answer: change in cost in C$ = ? = original cost in C$ – new cost in C$
Let’s consider original cost in C$. Here we have the original rate of C$ : US$ = 1 : 1.0218. Also, the manufacturer is buying the US currency to buy the product in US$, so sell rate applies: sell rate = (1+0.015)( orig. mid-rate).
Since
[latex]{\text{new currency amount}}=({\text{exchange rate}}_{orig \to new})({\text{original currency amt}})[/latex]
we have
[latex]{\text{US\$ amount}}=({\text{orig. sell rate}}_{C$ \to US$})({\text{C\$ amount}})[/latex]
Therefore,
[latex]\begin{align*} \text{C\$ amount}&=\frac{\text{US\$ amount}}{{\text{orig. sell rate}}_{C$ \to US$}}\\\\ &=\frac{7.25\cdot 100000}{(1+0.015)\cdot 1.0218}\\\\ &=\text{C\$ }699\,046.50 \end{align*}[/latex]
Let’s now consider the new cost in C$. We will again have to apply the sell rate, but this time the exchange rate has appreciated by 0.0178.
Therefore,
[latex]\begin{align*} \text{C\$ amount}&=\frac{\text{US\$ amount}}{{\text{new sell rate}}_{C$ \to US$}}\\\\ &=\frac{7.25\cdot 100000}{(1+0.015)\cdot (1.0218+0.0178)}\\\\ &=\text{C\$ }687\,077.45 \end{align*}[/latex]
So we can see that, due to the appreciation of Canadian dollar, the manufacturer has its input costs decrease by $11,969.05 since C$1 now purchases more US$.
Give it a Thought Answers
- a. More, since C$1 becomes US$1.0218; b. More, since AU$1 becomes MXN$12.5814; c. More, since MXN$1 becomes ¥6.7540; d. Less, since C$1 becomes €0.7137
- a. US dollars; b. Increase; c. Mexican pesos; d. Decrease
Chapter 5 Case Study: Completing Summary Financial Reports
The Situation
An accountant at Lightning Wholesale needs to summarize the GST remittances, costs of goods sold, and sales for 2013 by quarter. The table below presents the purchases (in US$) that it made from its American supplier, average monthly supplier cash discounts, total monthly sales (in C$), and the average monthly exchange rate appreciation or depreciation.
The data:
| Quarter | Month | 2013 | Average | 2013 | C$ |
| Purchases in US$ Before Discounts | Cash Discount | Sales in C$ | Appreciation ( ) or Depreciation (−) Against US$ | ||
| I | January | $2,021 | 2.00% | $1,798 | Start: 0.9423 |
| February | $2,200 | 3.00% | $2,407 | 1.00% | |
| March | $2,531 | 2.50% | $2,568 | –0.50% | |
| II | April | $2,623 | 1.50% | $2,985 | 0.35% |
| May | $2,676 | 1.00% | $3,114 | –1.50% | |
| June | $2,805 | 2.00% | $3,242 | 1.75% | |
| III | July | $3,309 | 2.25% | $3,306 | 1.00% |
| August | $4,146 | 2.00% | $3,852 | 0.50% | |
| September | $6,196 | 3.00% | $4,815 | –1.40% | |
| IV | October | $10,981 | 3.00% | $7,222 | –0.30% |
| November | $8,332 | 3.25% | $12,839 | 0.90% | |
| December | $1,520 | 1.75% | $9,630 | –0.75% |
(all figures are in thousands of dollars)
Important Information
- The imported products require GST to be paid on the equivalent Canadian value of the imported goods before any discounts.
- All sales are subject to GST.
- Lightning Wholesale’s suppliers offer it various cash discounts, which the accounting department always takes advantage of. These discounts have not been deducted from the purchase amounts listed in the table.
Your Tasks
- Calculate the exchange rates for each month throughout the 2013 operating year. Round all exchange rates to four decimals before calculating the next exchange rate.
- Compute quarterly GST remittances.
- Convert monthly purchases into Canadian funds and determine the monthly GST paid to the CBSA (Canada Border Services Agency).
- Assess the monthly GST collected on all sales.
- Complete a quarterly GST remittance table summarizing GST paid, GST collected, and the net amount refunded or remitted in 2013.
- Create a quarterly cost of goods sold and revenue table.
- Apply the average monthly cash discount to the Canadian monthly purchases amounts. Round all answers to the nearest thousands of dollars.
- Create a quarterly table summarizing costs of goods sold and sales with yearly totals of each.
Section Exercises – after the reading
Work on section 5.3 exercises in Fundamentals of Business Math Exercises after reading this section. Discuss your solutions with your peers and/or course instructor.
You may consult answers to select exercises: Fundamentals of Business Math Exercises – Select Answers