8.3 Quadratic Functions
Quadratic functions, also called quadratics, are transformations of the function [latex]f(x)=x^2[/latex] and in that way they are simply combinations of shifts, stretches or compressions, and/or reflections of the original parabola [latex]f(x)=x^2[/latex], producing yet another parabola.
Every function that can be written in the form [latex]f(x)=ax^2+bx+c[/latex] for some real numbers [latex]a, b[/latex] and [latex]c[/latex] where [latex]a\neq 0[/latex] is a quadratic function and every quadratic function can be written in this form.
So if you are looking at a parabola, you are looking at a quadratic function. If you are looking at a function whose formula can be written as [latex]f(x)=ax^2+bx+c[/latex], then you are looking at a quadratic function.
Quadratics in business commonly arise from problems involving revenue and profit, but also in other contexts, such as those involving surface areas of geometric shapes.
Example 1
A farmer wants to enclose a rectangular space in her backyard for a new garden. She has purchased 80 feet of wire fencing to enclose three sides, and will put the fourth side against the backyard fence. Find the function that describes the area enclosed by the fence in terms of the length [latex]l[/latex] of the sides of fencing perpendicular to the existing fence, and describe its domain.
Answer: The task is to find the function that calculates the area enclosed by the fence. Since the area of enclosed by the fence is rectangular, it depends on its length and width, [latex]l[/latex] and [latex]w[/latex], where [latex]l[/latex] is perpendicular and [latex]w[/latex] is parallel to the backyard fence. In a scenario like this involving geometry, it is often helpful to draw a picture and mark on it all relevant variables.
We know that the area of a rectangle can be represented by [latex]A=l\cdot w[/latex]. However, our task is to determine the area only using [latex]l[/latex] and so we must find a way to represent [latex]w[/latex] using [latex]l[/latex].
We are given a condition on the total length of the fence, which is 80 feet, and so we have that [latex]l+w+l=80[/latex]. We can rearrange this equation to solve for [latex]w[/latex]:
[latex]\begin{align*} l+w+l=80\Rightarrow &2l+w=80\\ \Rightarrow &w=80-2l \end{align*}[/latex]
So [latex]A=lw=l(80-2l)[/latex].
We can see that, using the above relationship, [latex]A[/latex] can be calculated for any value of [latex]l[/latex], but [latex]l[/latex] represents length of side so it must be greater than zero, and so the domain of [latex]A[/latex] is [latex](0, \infty)[/latex].
Therefore [latex]A(l)=l(80-2l) =80l-2l^2,\quad l>0[/latex].
This function represents the area [latex]A[/latex] of the fence in terms of the length [latex]l[/latex] of the fence side perpendicular to the existing fence. It is a quadratic function because it can be rewritten as [latex]A(l)=-2l^2+80l+0[/latex].
Example 2
A local newspaper currently has 84,000 subscribers, at a quarterly subscription price of $30. Market research has suggested that if they raised the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, create an equation to model their revenue as a function of the quarterly subscription price and determine the domain of the revenue function.
Answer:
Task: Determine the revenue as a function of the quarterly subscription price and identify its domain.
Revenue is the amount of money a company gets from sales, in other words, number of units sold times price per unit. In this case, the revenue can be found by multiplying the subscription price with the number of subscribers. To abbreviate this statement we can introduce variables, [latex]p[/latex] for price per subscription and [latex]n[/latex] for the number subscribers, giving us the equation:
[latex]\text{Revenue}=p\cdot n[/latex]
We now have the revenue expressed in terms of both the quarterly subscription price and the number of subscribers, while our task is to represent the revenue only in terms of the price. This means we have to find a way to represent the number of subscribers in terms of the price, which will allow us to replace [latex]n[/latex] in the revenue equation with values only involving [latex]p[/latex].
Finding [latex]n(p)[/latex]: Since the information given tells us the number of subscribers changes with the subscription price in a particular way, we can potentially find a relationship between these two variables using that condition, giving us the price-demand relationship. Because the number of subscriptions is linearly related to the subscription fee, we know that we can write [latex]n=mp+b[/latex] for some values [latex]m[/latex] and [latex]b[/latex] where [latex]m[/latex] is the rate of change in the number of subscribers relative to price, and [latex]b[/latex] is the value of the function when input is zero, i.e., the number of subscribers when the price is brought down to $0.00 (i.e., subscriptions become free).
To figure out the rate of change in the number of subscribers relative to price, which is [latex]m =\frac{\text{change in output}}{\text{change in input}}[/latex], we need two corresponding [latex](p,n)[/latex] pairs. We know that currently [latex]n = 84,000[/latex] and [latex]p = 30[/latex], and that if they raise the price to $32 they would lose 5,000 subscribers, giving a second pair of values, [latex]n = 79,000[/latex] and [latex]p = 32[/latex]. From this we can find a linear equation relating the two quantities. Thus, the rate of change in the number of subscribers per $ change in price is:
[latex]m = \dfrac{\Delta\text{output}}{\Delta\text{input}}=\dfrac{n_2-n_1}{p_2-p_1}=\dfrac{79,000 - 84,000}{32-30} = \dfrac{-5,000}{2} = -2,500[/latex]
This tells us the paper will lose 2,500 subscribers for each dollar increase in price. It also represents the slope of this price-demand graph. We can then solve for the value of [latex]b[/latex], i.e., the vertical intercept of the price-demand graph,
[latex]n = -2500p + b[/latex]
Use the input-output pair [latex]n = 84,000[/latex] and [latex]p = 30[/latex]:
[latex]84000 = -2500(30) + b[/latex]
Solve for [latex]b[/latex]:
[latex]b = 159,000[/latex]
This gives us the linear equation [latex]n = -2,500p + 159,000[/latex] relating price and subscription demand. We now return to our revenue equation.
[latex]\text{Revenue} = p\cdot n =p(-2,500p + 159,000)=-2,500p^2 + 159,000p[/latex]
To determine the domain of [latex]R(p)[/latex], we can see that [latex]R(p)[/latex] can be calculated for any [latex]p[/latex], but price can’t be negative, and so [latex]p\geq 0[/latex].
In addition, the revenue can’t be negative, so the value of [latex]p[/latex] should produce a nonnegative revenue. Since [latex]p\geq 0[/latex] and [latex]R(p)=p\cdot n(p)\geq 0[/latex], we must have that [latex]n(p)\geq 0[/latex]. Thus:
[latex]n(p)\geq 0\Rightarrow -2,500p + 159,000\geq 0\Rightarrow -2500p\geq 159000\Rightarrow p\leq 63.6[/latex]
[latex]\Rightarrow 0\leq p\leq 63.6[/latex]
Therefore revenue from the subscriptions can be modeled as function of the quarterly subscription price, given that the price is between $0 and $63.60 per subscription, as
[latex]R(p)=-2,500p^2 + 159,000p,\quad 0\leq p\leq 63.6[/latex]
Note that this is a quadratic function because it has a quadratic form: [latex]R(p)=-2,500p^2 + 159,000p+0[/latex]. Later in the course we will use functions like these to determine the price to charge to maximize revenue or profit.
Example 2: Alternative solution (using math symbols)
Same problem as above. Compare step by step the text solution above with the solution below that uses primarily math symbols, and thus it is much shorter.
A local newspaper currently has 84,000 subscribers, at a quarterly subscription price of $30. Market research has suggested that if they raised the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, create an equation to model their revenue as a function of the quarterly subscription price and determine the domain of the revenue function.
Answer:
Task: [latex]R(p)=?[/latex], domain of [latex]R(p)=?[/latex], revenue [latex]=R[/latex], quarterly subscription price [latex]=p[/latex]
[latex]p[/latex] input, [latex]R[/latex] output, revenue = (price per unit)(number of units)
[latex]\Rightarrow R(p)=p\cdot n[/latex] where [latex]n=n(p)[/latex] is number of subscriptions and a function of [latex]p[/latex].
[latex]n(p)=?[/latex]
[latex]n[/latex] output, [latex]p[/latex] input, constant rate of change, so linearly related [latex]\Rightarrow n(p)=mp+b[/latex] for some [latex]m[/latex] and [latex]b[/latex].
We have [latex](p_1,n_1)=(30, 84000)[/latex] and [latex](p_2,n_2)=(32,79000)[/latex] and so
[latex]m=\dfrac{\Delta\text{output}}{\Delta\text{input}}=\dfrac{n_2-n_1}{p_2-p_1}=\dfrac{79000-84000}{32-30}=-2500[/latex]
[latex]\Rightarrow n(p)=-2500p+b[/latex]
[latex]b=?[/latex]
[latex]n(30)=84000\Rightarrow -2500(30)+b=84000\Rightarrow b=159000[/latex]
[latex]\Rightarrow n(p)=-2500p+159000[/latex]
[latex]\Rightarrow R(p)=p\cdot n(p)=p(-2500p+159000)=-2500p^2+159000p[/latex]
[latex]\text{domain}=?[/latex] all possible input values
Price non-negative [latex]\Rightarrow p\geq 0[/latex]
Revenue non-negative and [latex]p\geq 0\Rightarrow R(p)=p\cdot n(p)\geq 0\Rightarrow n(p)\geq 0[/latex]
[latex]\Rightarrow -2,500p + 159,000\geq 0\Rightarrow -2500p\geq 159000\Rightarrow p\leq 63.6[/latex]
[latex]\Rightarrow 0\leq p\leq 63.6\Rightarrow \text{domain}=[0,63.6][/latex]
Therefore the revenue can be modeled by
[latex]R(p)=-2,500p^2 + 159,000p,\quad 0\leq p\leq 63.6[/latex]
where [latex]R(p)[/latex] is the revenue if [latex]p[/latex] is the price charged for a quarterly subscription, valid for price values between $0 and $63.60 per quarterly subscription.
Different Forms of a Quadratic Function
Every quadratic function can be represented through its standard form:
[latex]f(x)=ax^2+bx+c[/latex]
where [latex]a, b[/latex] and [latex]c[/latex] are real numbers and [latex]a\neq 0[/latex]. The value [latex]a[/latex] is called the leading coefficient and [latex]c[/latex] is the constant term.
Every quadratic function can also be represented through its vertex form:
[latex]f(x)=a(x-x_0)^2+y_0[/latex]
where [latex]a, x_0[/latex] and [latex]y_0[/latex] are real numbers and [latex]a\neq 0[/latex]. The values [latex]x_0[/latex] and [latex]y_0[/latex] represent the coordinates of the vertex [latex](x_0,y_0)[/latex] of the function.
Some quadratic functions can also be represented through the factored form:
[latex]f(x)=a(x-x_1)(x-x_2)[/latex]
where [latex]a, x_1[/latex] and [latex]x_2[/latex] are real numbers and [latex]a\neq 0[/latex]. The values [latex]x_1[/latex] and [latex]x_2[/latex] represent the zeros of the function, i.e., the input values making the value of the function 0 or, graphically, where the graph of the function crosses the horizontal axis.
The most commonly used form of a quadratic equation is the standard form but each one, standard, vertex and factored form, can be useful in different contexts because they provide direct information about the behaviour of the quadratic function:
- The standard form provides information about the orientation of the graph ([latex]a[/latex]) and its vertical intercept ([latex]c[/latex]).
- The vertex form provides information about the orientation of the graph ([latex]a[/latex]) and the highest (or lowest) point on its graph (vertex [latex](x_0,y_0)[/latex])
- The factored form gives us the information about the orientation of the graph ([latex]a[/latex]) and where the graph intercepts the horizontal axis ([latex]x_1[/latex] and [latex]x_2[/latex]).
There are six types of graphs arising from quadratic equations, determined by the orientation of the parabola and the location of the vertex, which together determine how how many zeros the function has (two, one or none):
Example 3
Determine the orientation, the vertical intercept, the coordinates of the vertex and the horizontal intercepts of the quadratic function, and sketch its graph if its standard, vertex and factored form are
[latex]\begin{align*} f(x)&=-\frac{1}{5}x^2-\frac{2}{5}x+\frac{8}{5}&\text{standard form} \\ &=-\frac{1}{5}(x+1)^2+\frac{9}{5}&\text{vertex form}\\ &=-\frac{1}{5}(x-2)(x+4)&\text{factored form} \end{align*}[/latex]
Answer: From standard form [latex]f(x)=ax^2+bx+c[/latex] we can see that the parabola is oriented downwards because the leading coefficient, i.e., the coefficient of [latex]x^2[/latex], is [latex]-\frac{1}{5}[/latex], which is a negative number. Also, since the constant term in the standard form, i.e., the term with no variable, is [latex]\frac{8}{5}[/latex], the vertical intercept is at the point [latex]\left(0, \frac{8}{5}\right)[/latex].
The vertex form [latex]f(x)=a(x-x_0)^2+y_0[/latex] tells us that [latex]x-x_0=x+1[/latex] and that [latex]y_0=\frac{9}{5}[/latex], and so [latex]x_0=-1[/latex] and [latex]f(x_0)=y_0=\frac{9}{5}[/latex]. Therefore, the vertex is at the point [latex]\left(-1,\frac{9}{5}\right)[/latex].
Finally, the factored form [latex]f(x)=a(x-x_1)(x-x_2)[/latex] tells us that [latex]x-x_1=x-2[/latex] and [latex]x-x_2=x+4[/latex] and so [latex]x_1=2[/latex] and [latex]x_2=-4[/latex]. Therefore, the zeros of the function are 2 and -4 and so the horizontal intercepts are at points [latex](2,0)[/latex] and [latex](-4,0)[/latex].
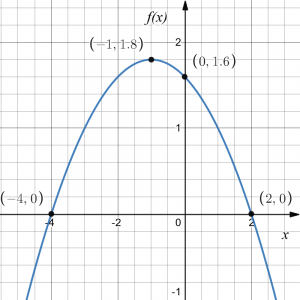
Finding the vertex and the zeros of a quadratic function
Given the quadratic function in its standard form [latex]f(x)=ax^2+bx+c[/latex], its vertex coordinates [latex](x_0,y_0)[/latex] can be calculated as follows:
[latex]\begin{align*} x_0&=-\frac{b}{2a}\\ y_0&=f(x_0) \end{align*}[/latex]
If the quadratic function has zeros (remember that not every quadratic function does), its zeros [latex]x_1[/latex] and [latex]x_2[/latex] can be calculated using the quadratic formula:
[latex]x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}[/latex]
Note that this is the abbreviated version of writing [latex]x_{1}=\frac{-b+ \sqrt{b^2-4ac}}{2a}[/latex] and [latex]x_{2}=\frac{-b- \sqrt{b^2-4ac}}{2a}[/latex]. Also note that there are no zeros if the expression [latex]b^2-4ac[/latex], also called the discriminant, is a negative number.
If the quadratic functions has zeros, say [latex]x_1[/latex] and [latex]x_2[/latex], then it can be factored as follows:
[latex]f(x)=a(x-x_1)(x-x_2)[/latex] where [latex]x_{1,2}=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}[/latex]
It is very important to note that the quadratic formula solves the equation [latex]ax^2+bx+c=0[/latex], i.e., determines the values of [latex]x[/latex] that satisfy [latex]f(x)=0[/latex]. There are other methods for solving a quadratic equation that can be used in some special cases, but the quadratic formula will always work if there are solutions.
Example 4
Find the vertex and the vertical and horizontal intercepts of the quadratic [latex]f(x)=3x^2+5x-2[/latex] and determine the factored form of [latex]f(x)[/latex].
Answer:
vertex: We can use the standard form in which [latex]f(x)[/latex] is written and so the vertex is located at [latex](x_0,f(x_0))[/latex] where
[latex]x_0=-\dfrac{b}{2a}=-\dfrac{5}{2\cdot(3)}=-\dfrac{5}{6}[/latex]
Since
[latex]f\left(-\dfrac{5}{6}\right)=3\left(-\dfrac{5}{6}\right)^2+5\left(-\dfrac{5}{6}\right)-2=-\dfrac{49}{12}[/latex]
the vertex is located at the point [latex]\left(-\frac{5}{6},-\frac{49}{12}\right)[/latex].
vertical intercept: The vertical intercept occurs when the input value is zero:
[latex]f(0)=3(0)^2+5(0)-2=-2[/latex]
Equivalently, we can use the standard form of [latex]f(x)[/latex] and the fact that the vertical intercept occurs at [latex](0,c)[/latex], and so the vertical intercept is at (0,-2).
horizontal intercepts: The horizontal intercepts occur when the output is zero, i.e., [latex]f(x)=0[/latex]:
[latex]0=3x^2+5x-2.[/latex]
To solve this equation we can use the quadratic formula:
[latex]\begin{align*} x_{1,2}&=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\\ & =\frac{-5\pm \sqrt{5^2-4\cdot 3\cdot (-2)}}{2\cdot 3}\\ &=\frac{-5\pm 7}{6}\\ \Rightarrow&x_1=\frac{-5+ 7}{6}=\frac{1}{3}\\ &x_2=\frac{-5-7}{6}=-2 \end{align*}[/latex]
So the horizontal intercepts are at [latex]\left(\frac{1}{3},0\right)[/latex] and [latex](-2,0)[/latex].
factored form: Using the fact that [latex]x_1=\frac{1}{3}[/latex] and [latex]x_2=-2[/latex] are the zeros of the quadratic function [latex]f(x)[/latex], we can rewrite [latex]f(x)[/latex] as
[latex]f(x)=a(x-x_1)(x-x_2)=3\left(x-\frac{1}{3}\right)(x+2)[/latex]
You can verify all of the above by using a graphing calculator, say Desmos: link, however you must be able to justify all characteristics algebraically as above.
Section Exercises
Work on section 8.3 exercises in Fundamentals of Business Math Exercises. Discuss your solutions with your peers and/or course instructor.
You may consult answers to select exercises: Fundamentals of Business Math Exercises – Select Answers
