8.1 Functions
Section Exercises – after the reading
Work on section 8.1 exercises in Fundamentals of Business Math Exercises after reading this section. Discuss your solutions with your peers and/or course instructor.
You may consult answers to select exercises: Fundamentals of Business Math Exercises – Select Answers
What is a function?
The natural world is full of relationships between quantities that change. When we see these relationships, it is natural for us to ask: If I know one quantity, can I then determine the other? This establishes the idea of an input quantity, or independent variable, and a corresponding output quantity, or dependent variable. From this we get the notion of a functional relationship in which the output can be determined from the input.
Concept Check
Can you determine what is input and what is output in a relationship? Which value in a relationship represents the independent and which represents the dependent variable? Try this quick set of multiple choice exercises:
MathMatize: Independent vs. dependent variables
For some quantities, like height and age, there are certainly relationships between these quantities. Given a specific person and any age, it is easy enough to determine their height, but if we tried to reverse that relationship and determine height from a given age, that would be problematic since most people maintain the same height for many years.
In this course we will be working with relationships of the first type, where for each input value we get one and only one output value. In other words, there is no ambiguity about the result – it is uniquely determined by the given information, or input. These types of relationships are called functions and have many very useful properties that will allow us to study those relationships in great detail.
Function
A function is rule for a relationship between an input, or independent, quantity and an output, or dependent, quantity in which each input value uniquely determines one output value. We say “the output is a function of the input.”
Example 1
Is height a function of age? Is age a function of height?
Answer: In the height and age example above, it would be correct to say that height is a function of age since each age uniquely determines a height. For example, on my 18th birthday I had exactly one height of 69 inches.
However, age is not a function of height since one height input might correspond with more than one output age. For example, for an input height of 70 inches, there is more than one output of age since I was 70 inches at the age of 20 and 21.
Concept Check
Can you determine if a relationship could be represented as a function or possibly not? Test your understanding of the concept of function through these quick multiple choice and fill-in-the-blank exercises:
MathMatize: Function or not?
Function Notation
As you can see from Concept Check exercises above, talking about relationships can get quite “wordy”. To simplify writing out expressions and equations involving functions, a simplified notation is often used. We also use descriptive variables to help us remember the meaning of the variables used in the problem.
Rather than write height is a function of age, we could use the descriptive variable [latex]h[/latex] to represent height and we could use the descriptive variable [latex]a[/latex] to represent age. We can then simply write [latex]h(a)[/latex] to say “height is a function of age”.
Remember we can use any variable to name the function; the notation [latex]h(a)[/latex] shows us that [latex]h[/latex] depends on [latex]a[/latex]. The value [latex]a[/latex] must be put into the function [latex]h[/latex] to get a result. Be careful – the parentheses indicate that age is input into the function (note: do not confuse these parentheses with multiplication!).
Function Notation
Example 2
A function [latex]N = f(y)[/latex] gives the number of police officers, [latex]N[/latex], in a town in year [latex]y[/latex]. What does [latex]f(2005) = 300[/latex] tell us?
Answer: When we read [latex]f(2005) = 300[/latex], we see the input quantity is 2005, which is a value for the input quantity of the function, the year ([latex]y[/latex]). The output value is 300, the number of police officers ([latex]N[/latex]), a value for the output quantity. Remember [latex]N=f(y)[/latex]. So this tells us that in the year 2005 there were 300 police officers in the town.
Concept Check
Function notation can be confusing. Check if you are on the right track connecting words to symbols and symbols to words when discussing relationships represented through functions:
Try MathMatize: Function notation
Tables as Functions
Functions can be represented in many ways: words (as we did in the last few examples), tables of values, graphs, or formulas. Represented as a table, we are presented with a list of input and output values.
Important note: by convention, the first row (or column) in a table represents the independent variable.
This table represents the age of children in years and their corresponding heights. While some tables show all the information we know about a function, this particular table represents just some of the data available for height and ages of children.
| (input) [latex]a[/latex], age in years | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| (output) [latex]h[/latex], height in inches | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Example 3
Which of these tables define a function (if any)?
| Input | Output |
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Input | Output |
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Input | Output |
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Answer: The first and second tables define functions. In both, each input corresponds to exactly one output. The third table does not define a function since the input value of 5 corresponds with two different output values.
Solving and Evaluating Functions
When we work with functions, there are two typical things we do: evaluate and solve.
Evaluating a function is what we do when we know an input, and use the function to determine the corresponding output. Evaluating will always produce one result, since each input of a function corresponds to exactly one output.
Solving equations involving a function is what we do when we know an output, and use the function to determine the inputs that would produce that output. Solving a function could produce more than one solution, since different inputs can produce the same output.
Example 4
Using the table shown, where [latex]Q=g(n)[/latex]
| [latex]n[/latex] | 1 | 2 | 3 | 4 | 5 |
| [latex]Q[/latex] | 8 | 6 | 7 | 6 | 8 |
a) Evaluate [latex]g(3)[/latex].
b) Solve [latex]g(n)=6[/latex].
Answer:
a) Evaluate [latex]g(3)[/latex]: Evaluating [latex]g(3)[/latex] (read: g of 3) means that we need to determine the output value, [latex]Q[/latex], of the function [latex]g[/latex] given the input value of [latex]n=3[/latex]. Looking at the table, we see the output corresponding to [latex]n=3[/latex] is [latex]Q=7[/latex], allowing us to conclude [latex]g(3) = 7[/latex].
b) Solve [latex]g(n)=6[/latex]: Solving [latex]g(n) = 6[/latex] means we need to determine what input values, [latex]n[/latex], produce an output value of 6. Looking at the table we see there are two solutions: [latex]n = 2[/latex] and [latex]n = 4[/latex]. When we input 2 into the function [latex]g[/latex], our output is [latex]Q = 6[/latex]. When we input 4 into the function [latex]g[/latex], our output is also [latex]Q = 6[/latex].
Concept Check
Here are some examples relationships represented using tables. Which ones of them represent functions?
MathMatize: Functions from data tables
Graphs as Functions
Oftentimes a graph of a relationship can be used to define a function. By convention, graphs are typically created with the input quantity along the horizontal axis and the output quantity along the vertical.
Example 5
Which of these graphs defines a function [latex]y=f(x)[/latex]?

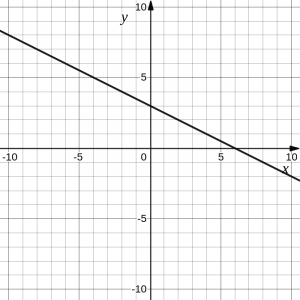
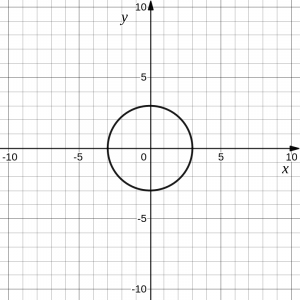
Answer:
Looking at the three graphs above, the first two define a function [latex]y=f(x)[/latex], since for each input value along the horizontal axis there is exactly one output value corresponding, determined by the [latex]y[/latex]-value of the graph. The third graph does not define a function [latex]y=f(x)[/latex] since some input values, such as [latex]x=2[/latex], correspond with more than one output value.
Vertical Line Test
Reading Graphs of Functions
Evaluating a function using a graph requires taking the given input (horizontal axis) and using the graph to look up the corresponding output. Solving a function equation using a graph requires taking the given output and looking on the graph to determine the corresponding input.
Example 6
Consider the graph below.

a) Evaluate [latex]f(2)[/latex].
b) Solve [latex]f(x) = 4[/latex].
Answer:
a) To evaluate [latex]f(2)[/latex], we find the input of [latex]x=2[/latex] on the horizontal axis. Moving up to the graph gives the point (2, 1), giving an output of [latex]f(x)=1[/latex]. So [latex]f(2) = 1[/latex].
b) To solve [latex]f(x) = 4[/latex], we find the value 4 on the vertical axis because if [latex]f(x) = 4[/latex] then 4 is the output. Moving horizontally across the graph gives two points with the output of 4: [latex](-1,4)[/latex] and [latex](3,4)[/latex]. These give the two solutions to [latex]f(x) = 4[/latex]: [latex]x = -1[/latex] or [latex]x = 3[/latex]. This means [latex]f(-1)=4[/latex] and [latex]f(3)=4[/latex], or when the input is -1 or 3, the output is 4.
Note that while the graph in the previous example is a function, getting two input values for the output value of 4 shows us that this function is not one-to-one, i.e., there are two or more inputs that map to the same output. This, in turn, means this relationship cannot be reversed, i.e., [latex]f[/latex] is a function of [latex]x[/latex], but [latex]x[/latex] is not a function of [latex]f[/latex] because otherwise there would be input values [latex]f[/latex] giving more than one output [latex]x[/latex]. On the other hand, if a function is one-to-one, i.e., no output values are repeated, then the function is invertible.
Formulas as Functions
When possible, it is very convenient to define relationships using formulas. If it is possible to express the output as a formula involving the input quantity, then we can define a function.
Concept in Action – Demo by Video
Example 7
Express the relationship [latex]2n + 6p = 12[/latex] as a function [latex]p(n)[/latex] if possible.
Answer:
To express the relationship in this form, we need to be able to write the relationship where [latex]p[/latex] is a function of [latex]n[/latex], which means writing it as [latex]p =[/latex] [something involving [latex]n[/latex]].
[latex]\begin{align*}&2n + 6p = 12\\ &\Rightarrow 6p = 12 - 2n\\ &\Rightarrow p=\frac{12-2n}{6}=\frac{12}{6}-\frac{2n}{6}=2-\frac{1}{3}n \end{align*}[/latex]
Having rewritten the formula to solve for [latex]p[/latex], we can now express [latex]p[/latex] as a function of [latex]n[/latex]:
[latex]p(n)=2-\frac{1}{3}n[/latex]
Not every relationship can be expressed as a function with a formula.
As with tables and graphs, it is common to evaluate and solve functions involving formulas. Evaluating a function will require replacing the input variable in the formula with the value provided and calculating the value of the expression. Solving a function will require replacing the output variable in the formula with the value provided, and rearranging the function formula to solve for the input(s) that would produce that output.
Example 8
Given the function [latex]k(t)=t^3+2[/latex]:
a) Evaluate [latex]k(2)[/latex].
b) Solve [latex]k(t)=1[/latex].
Answer:
a) To evaluate [latex]k(2)[/latex], we plug in the input value 2 into the formula wherever we see the input variable [latex]t[/latex], then simplify:
[latex]k(2) = 2^3+2 = 8+2 =10[/latex]
So [latex]k(2) = 10[/latex].
b) To solve [latex]k(t) = 1[/latex], we set the formula for [latex]k(t)[/latex] equal to 1, and solve for the input value that will produce that output:
[latex]\begin{align*} k(t) &= 1 & \\ &\Rightarrow t^3+2 = 1 &\text{substitute the original formula} \\ &\Rightarrow t^3 = -1 &\text{subtract 2 from each side} \\ &\Rightarrow t = -1 &\text{take the cube root of each side} \end{align*}[/latex]
When solving an equation using formulas, you can check your answer by using your solution in the original equation to see if your calculated answer is correct.
We want to know if [latex]k(t) = 1[/latex] is true when [latex]t=-1[/latex]:
[latex]\begin{align*}k(-1) & = (-1)^3+2\\ & = -1+2\\ & = 1\end{align*}[/latex]
which was the desired result.
Basic Function Types
There are some basic functions that one should know and be able to recognize through name and shape. General functions will often come from these basic types through various operations and transformations. These basic types are listed below and for their definitions we will use [latex]x[/latex] as the input variable and [latex]f(x)[/latex] as the output variable.
Basic functions
| Constant: | [latex]f(x)=c[/latex], where [latex]c[/latex] is a constant (number) |
| Identity: | [latex]f(x)=x[/latex] |
| Absolute Value: | [latex]f(x)=|x|[/latex] |
| Quadratic: | [latex]f(x)=x^2[/latex] |
| Cubic: | [latex]f(x)=x^3[/latex] |
| Reciprocal: | [latex]f(x)=\frac{1}{x}[/latex] |
| General reciprocal: | [latex]f(x)=\frac{1}{x^2}[/latex] |
| Square root: | [latex]f(x)=\sqrt[2]{x}=\sqrt{x}[/latex] |
| Cube root: | [latex]f(x)=\sqrt[3]{x}[/latex] |
Graphs of the Basic Types of Functions

Constant, [latex]f(x)=c[/latex] (c is 2 in this picture).
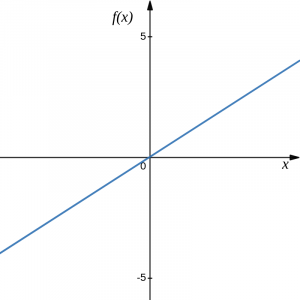
Identity: [latex]f(x)=x[/latex].
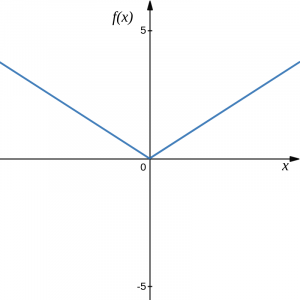
Absolute Value: [latex]f(x)=|x|[/latex]
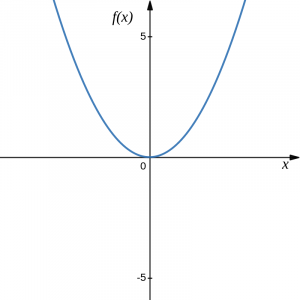
Quadratic: [latex]f(x)=x^2[/latex]
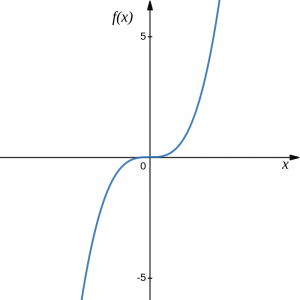
Cubic: [latex]f(x)=x^3[/latex]
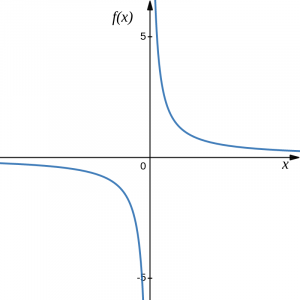
Reciprocal: [latex]f(x)=\frac{1}{x}[/latex]
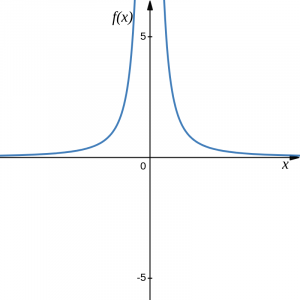
Reciprocal squared: [latex]f(x)=\frac{1}{x^2}[/latex]
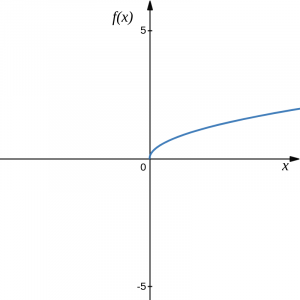
Square root: [latex]f(x)=\sqrt[2]{x}=\sqrt{x}[/latex]
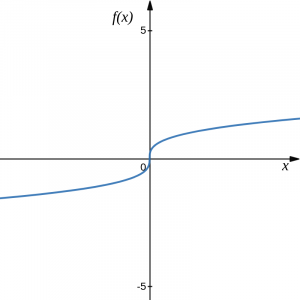
Cube root: [latex]f(x)=\sqrt[3]{x}[/latex]
Concept in Action - Visualization
See these functions for yourself:
Geogebra: Basic types of functions (click on circle beside the function whose graph you would like to explore)
One of our main goals in mathematics is to model the real world with mathematical functions. In doing so, it is important to keep in mind the limitations of those models we create.
This table shows a relationship between circumference and height of a tree as it grows.
| Circumference, [latex]c[/latex] | 1.7 | 2.5 | 5.5 | 8.2 | 13.7 |
| Height, [latex]h[/latex] | 24.5 | 31 | 45.2 | 54.6 | 92.1 |
While there is a strong relationship between the two, it would certainly be ridiculous to talk about a tree with a circumference of -3 feet, or a height of 3000 feet. When we identify limitations on the inputs and outputs of a function, we are determining the domain and range of the function.
Domain and Range
Range: The set of all possible output values of a function.
Example 9
Using the tree table above, determine a reasonable domain and range.
Answer:
We could combine the data provided with our own experiences and reason to approximate the domain and range of the function [latex]h = f(c)[/latex]. For the domain, possible values for the input circumference [latex]c[/latex], it doesn’t make sense to have negative values, so [latex]c > 0[/latex]. We could make an educated guess at a maximum reasonable value, or look up that the maximum circumference measured is about 119 feet. With this information we would say a reasonable domain is more than 0 and less than 120 feet.
Similarly for the range, it doesn’t make sense to have negative heights, and the maximum height of a tree could be looked up to be 379 feet, so a reasonable range is more than 0 and less than 380 feet.
A more compact alternative to inequality notation is interval notation, in which intervals of values are referred to by the starting and ending values. Curved parentheses are used for strictly less than, and square brackets are used for less than or equal to. Since infinity is not a number, we can’t include it in the interval, so we always use curved parentheses with [latex]\infty[/latex] and [latex]-\infty[/latex]. The curved parentheses are also referred to as open while the square ones are referred to as closed. The table below will help you see how inequalities correspond to interval notation:
| Inequality | Interval Notation |
| [latex]5 \lt h \leq10[/latex] | [latex](5, 10][/latex] |
| [latex]5 \lt h \lt 10[/latex] | [latex](5, 10)[/latex] |
| [latex]5\leq h \lt10[/latex] | [latex][5, 10)[/latex] |
| [latex]h \lt10[/latex] | [latex](-\infty,10)[/latex] |
| [latex]h\geq10[/latex] | [latex][10,\infty)[/latex] |
| All real numbers ([latex]\mathbb{R}[/latex]) | [latex](-\infty,\infty)[/latex] |
Example 10
Describe the intervals of values shown on the line graph below using set builder and interval notations:

Answer:
To describe the values of [latex]x[/latex] that lie in the intervals shown above we would say: [latex]x[/latex] is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.
Written as an inequality, it is [latex]1\leq x\leq 3[/latex] or [latex]x \gt 5[/latex].
Written in interval notation, it is [latex][1,3]\cup(5,\infty)[/latex].
Example 11
Find the domain of each function:
a) [latex]f(x)=2\sqrt{x+4}[/latex]
b) [latex]g(x)=\dfrac{3}{6-3x}[/latex]
Answer:
a) domain? ---> all input values that produce an output ---> all values of [latex]x[/latex] that produce a result using [latex]f(x)=2\sqrt{x+4}[/latex]
Hence we have to analyze how the input is used to produce an output in this case:
To produce [latex]f(x)[/latex] given a value for [latex]x[/latex], we first perform addition on [latex]x[/latex], which never causes an issue.
Then we take a square root, which is an even root, and so we have to make sure that what is underneath the root is greater or equal to zero, i.e., [latex]x+4\ge 0[/latex]. This is because we cannot take an even root of a negative number (note that this is not a problem for an odd root).
Finally, the last operation is multiplication (by 2) and, since multiplication never causes an issue, it does not give us additional restrictions.
Therefore, the only restriction we have on [latex]x[/latex] is that [latex]x+4\geq 0[/latex]. Hence [latex]x\geq -4[/latex], and so the domain of [latex]f(x)[/latex] is [latex][-4,\infty)[/latex].
b) domain? ---> all input values that produce an output ---> all values of [latex]x[/latex] that produce a result using [latex]g(x)=\dfrac{3}{6-3x}[/latex]
Hence we have to analyze how the input is used to produce an output in this case:
To produce [latex]g(x)[/latex] given a value for [latex]x[/latex], we first perform multiplication on [latex]x[/latex] by [latex]3[/latex] ([latex]3x[/latex]), which can be calculated for any value of [latex]x[/latex].
Then we perform subtraction ([latex]6-3x[/latex]), which also never causes problems.
Finally we perform division, which is fine for all values except for division by zero. We cannot get a result if we divide a number by zero and so we have to make sure that the denominator, in this case [latex]6-3x[/latex], is not zero. Hence,
[latex]6-3x\neq 0\Rightarrow -3x=-6\Rightarrow x\neq 2[/latex]
Therefore, the only restriction we have on [latex]x[/latex] is that [latex]x\neq 2[/latex]. Hence, the domain of [latex]g(x)[/latex] is [latex](-\infty,2)\cup(2,\infty)[/latex].
Example 12
A phone data plan has a basic charge of $30 a month. The plan includes first 2GB free and charges $10 for each additional GB, up to 8 GB total usage, after which it charges $15 for each additional GB. If [latex]d[/latex] is the amount of data used (in GB) and [latex]C[/latex] is the total monthly cost:
a. Express [latex]C(d)[/latex] as a (piece-wise) formula.
b. Identify the domain and range of [latex]C(d)[/latex].
c. Graph [latex]C[/latex] as a function of [latex]d[/latex] for [latex]0\le d\le 10[/latex].
d. Calculate the cost if 9GB were used.
Answer:
a. Task: [latex]C(d)=?[/latex]
Conditions:
only basic charge for first 2GB [latex]\Rightarrow C(d)=\underbrace{30}_{\text{basic charge}}, 0\le d\le 2[/latex]
after 2GB and up to 8 GB, charge of $10/GB for additional GB
[latex]\Rightarrow C(d)=\underbrace{30}_{\text{cost of first 2GB}}+\underbrace{10(d-2)}_{\text{cost above 2GB}}=10d+10, 2< d\le 8[/latex]
after 8GB, charge of $15/GB for additional GB
[latex]\Rightarrow C(d)=\underbrace{30+10(8-2)}_{\text{cost of first 8GB}}+\underbrace{15(d-8)}_{\text{cost above 8GB}}=15d-30, 2< d\le 8[/latex]
In piece-wise form:
[latex]C(d)=\begin{cases} 30 & 0\le d\le 2 \\ 10d+10& 2< d\le 8 \\ 15d-30 & 8< d \end{cases}[/latex]
b. domain: all possible input values
input: amount of data used [latex]d[/latex]
[latex]C(d)[/latex] can be calculated for any value of [latex]d[/latex] so [latex]d[/latex] can be any real number.
[latex]d=\text{amount of data used}\rightarrow[/latex] can't be negative, no upper limit [latex]\Rightarrow d\ge 0[/latex]
[latex]\Rightarrow domain = [0,\infty)[/latex]
range: all possible output values
output: cost [latex]C(d)[/latex]
cost is at least 30, no upper limit [latex]\Rightarrow C(d)\ge 30[/latex]
[latex]\Rightarrow range = [30,\infty)[/latex]
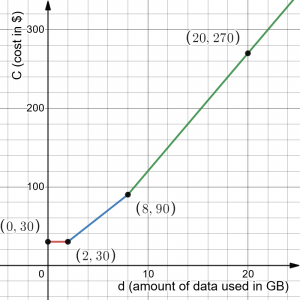
c. Each section is a linear function so we can graph each section by finding two points that belong to the respective lines:
[latex]\begin{align*} 0\le d\le 2&:C(0)=30; C(2)=30\\ 2< d\le 8&: C(2)=10\cdot 2+10=30; C(8)=10\cdot 8+10=90\\ d>8&:C(8)=15\cdot 8-30=90; C(20)=15\cdot 20-30=270 \end{align*}[/latex]
(Note that for the last section our choice for 20 as input was arbitrary; we could have picked any number greater than 8.)
So the graph looks as follows:
d. [latex]C(9)=?[/latex]
Since [latex]9>8[/latex], [latex]C(d)=15d-30[/latex] applies and so [latex]C(9)=15\cdot 9-30=105[/latex]. Hence the cost if 9GB are used is $105.
Concept Check
Test your understanding of the concepts discussed in this section: Functions as relationships
Section Exercises - after the reading
Work on section 8.1 exercises in Fundamentals of Business Math Exercises after reading this section. Discuss your solutions with your peers and/or course instructor.
You may consult answers to select exercises: Fundamentals of Business Math Exercises – Select Answers

