42 Fourier Transforms
With a Fourier Series that includes enough terms, you can model complex signals or multidimensional shapes as combinations of many sine and cosine signals. (video 8:24)
This is a mathematically difficult process that you don’t need to master in order to take advantage of the concepts. Signals contain high frequency elements related to the sudden changes and lower frequency elements related to changes that take place over time. You can also go in the opposite direction to decompose a time series signal into many Fourier components to identify dominant frequencies.
Finite Fourier Transforms of Time Series
If you have a finite number of data points in a time series, then you can generate a curve that runs through each of the points with a finite number of terms in a Fourier Series. The ability to draw the curve is not especially useful, as there are lots of easier ways to draw a curve through some data, however, a really valuable byproduct comes in determining the size of the contribution from different frequency components.
In a simple system we might find the natural frequency of oscillation by counting zero crossings, or peaks in the oscillating signal in response to a step function input. In a more realistic situation we may not be able to observe a step function response and there may be multiple frequencies present. For machine condition monitoring we might use dedicated hardware with the FFT capability built in. Changes in frequency characteristics give an early warning diagnostic and let us take a machine offline for maintenance before it fails – crucial for high reliability systems. (video 1:48)
https://www.youtube.com/watch?v=qz0MLVh7Gok
Fast Fourier Transform (FFT) Functions
If your time series data is uniformly spaced in time and the number of points is a power of 2, e.g. 64, 128, 256, 512, etc. points, you can take advantage of some symmetry to perform the transform calculations quickly (Cooley-Tukey 1965 if you really want details). Most engineers find these algorithms very useful without need to know their inner workings. The full FFT is done with complex (real and imaginary) numbers with a full floating point calculation that maintains phase information (separate sine and cosine series) while integer implementations that ignore the phase can run much faster. This video shows an example based on this code that shows an integer calculation completing about 20 times faster on a SAMD M0 processor. (video 7:01)
The signal at left shows three distinct frequencies, followed by the FFT trace in the middle shows three matching peaks. The red line is a full floating point complex FFT, while the green is the much faster 16 bit integer real version.
Choosing Sampling Parameters
The sampling frequency for the data defines the maximum detectable frequency. Since each cycle of a sine wave would require at least one point up and one point down to be visible, the maximum detectable frequency is half the sampling frequency, referred to as the Nyquist frequency.
(1) 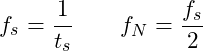
Accordingly, the FFT returns only half as many independent frequency components as there are points in the data, e.g. a 512 point FFT returns a zero frequency DC component and 256 components equally space between zero and the Nyquist frequency. Thus, the step between frequencies is
(2) 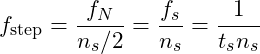
An FFT with ![]() points with data taken 100 times a second (
points with data taken 100 times a second (![]() Hz or
Hz or ![]() s) would return components 0 to 256 at frequencies of 0, 0.195, 0.391, 0.586, … 50.000.
s) would return components 0 to 256 at frequencies of 0, 0.195, 0.391, 0.586, … 50.000.
The number of points in the FFT determines the resolution of the results. Higher resolution is almost always good, but it comes at a cost of longer processing time. In a microcontroller system it is critical that we keep the looping rate high enough for good control, so we may need to pass the data to another processor for really detailed results.
Matching points and sampling frequency gives round frequency steps in the results. e.g. ![]() for results at frequencies of 0, 0.1, 0.2, 0.3, … 51.2 Hz.
for results at frequencies of 0, 0.1, 0.2, 0.3, … 51.2 Hz.
Subtract the mean to avoid a huge DC component at 0 Hz. Sine waves oscillate about zero. Make your signal oscillate about zero to reduce the first component of the FFT results so you can see the non-zero frequency components clearly. An easy way to do this is calculating the mean of all the points in your signal, then subtracting that value from each point. This simply offsets the signal and doesn’t change the shape or any of the frequency content.
This video (3:00) shows how to put these parameters into action to extract frequency data from a photocell input.

