Synopsis

• 16 bit unsigned short values go from 0 to 65535, while 32 bit unsigned long values go from 0 to more than 4 billion, and 64 bit long long integers are truly enormous.
• 16 bit short integers range from  -32768 to 32767 while 32 bit long integers cover more than +/- 2 billion, and 64 bit long long integers are truly enormous.
• 32 bit floating point numbers go from -3.4E+38 to 3.4E+38 with about 7 decimal digits of accuracy. Use double precision (64 bit) when you can to to provide about 16 decimal digits of accuracy over a range of 1E+308.
• Integer arithmetic rolls over and wraps around at the limits, resulting in some non-intuitive results that you’ll need to read the rest of the chapter to better understand. Most importantly integer division means 3/2 results in 1 in most languages, but not Python v3 or higher.

Introduction

You already have a basic familiarity with math and numbers that you have developed from many years in school. You know about Natural Numbers, Whole Numbers, Integers, Real Numbers (Rational and Irrational), and maybe even Imaginary and Complex Numbers. You have used calculators that almost always gave you the answer you expected.

Countable Units or Unsigned Integers

If we are counting oranges, the choices are 0, 1, 2, 3,… up to a very large number of oranges, and we could write each orange’s number on the side with a Sharpie. That way we know how many oranges and which is which, assuming for illustration that oranges can’t be divided into smaller slices. It makes sense to talk about orange number 5, but not orange number 5.67. Any time we are talking about countable units, it only makes sense to have 0 or more units, and we can represent the value as a decimal or binary whole number.

The maximum number we can count up to is determined by the number of decimal or binary digits we use to represent the number, e.g. we can only count to 999 on a three digit decimal display. A four bit binary number can range from 0b0000 (0 decimal) to 0b1111 (1+2+4+8 = 15 decimal), sometimes represented as a single hexadecimal digit (0,1,2,…9,A,B,C,D,E,F), e.g. 0xC.

• Eight bits make a byte, ranging from 0b00000000 to 0b11111111 (0xFF hex or 255 decimal), usually used to represent an ASCII character. Also referred to as uint8_t
• 16 bits is the size of an unsigned short integer value, ranging from 0x0000 to 0xFFFF 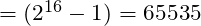Also referred to as uint16_t
• A 32 bit value is referred to as an unsigned long integer, ranging from 0x00000000 to 0xFFFFFFFF 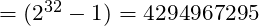Also referred to as uint32_t
• A 64 bit value is referred to as an unsigned long long integer, ranging from 0x0000000000000000 to 0xFFFFFFFFFFFFFFFF 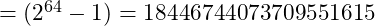, and may not be available on small processors like microcontrollers. Also referred to as uint64_t
• With enough storage space it is possible to exactly represent an unsigned integer of any size, but we can usually get by with numbers less than 4 billion.

Rollover in Counting and Calculations

When we hit the boundaries we could generate an error and stop the program, but the usual convention in integer arithmetic is to simply roll over the boundaries. This is easiest to understand with examples. Adding 1 each time would give these sequences for 4 and 8 bit number representations:

0b00001100

12

0b1100

12

0b00001101

13

0b1101

13

0b00001110

14

0b1110

14

0b00001111

15

0b1111

15

0b00010000

16

0b0000

0

0b00010001

17

0b0001

1

0b00010010

18

0b0010

2

0b00010011

19

0b0011

3

As the values increase some additions produce a ‘carry’, e.g. adding 1 to 0b1101 yields 0b1110 with 1+1 carrying over from the one’s column to the two’s column. At 0b1111 the 4 bit number is full, at its maximum value, and the next addition would produce a carry over to the 5th bit. That carry is successful in the 8 bit version, but just falls off the edge in the 4 bit version and the result is truncated to 0. The same thing happens with subtraction if you work your way up the table so that 0 – 1 yields 15 in the 4 bit column. The same mechanics apply at the upper and lower limits of larger representations using 8, 16, 32, or 64 bits to store the values.

Differences in Countable Units or Signed Integers

If we measure the difference in quantities between two piles of oranges, the difference can be positive or negative, but still has no fractional part.

The maximum number we can count up to is determined by the number of decimal or binary digits we use to represent the number, e.g. we can only count to 999 on a three digit decimal display. We need one more bit to represent the sign of the number. A four bit binary number will thus have only three bits for magnitude and one for the sign.

16 bits is the usual size of a short integer value, ranging from -32768 to +32767

A 32 bit value is usually referred to as a long integer, ranging from -2147483648 to 2147483647

Explicit size types of int8_t, int16_t, int32_t, or int64_t

With enough storage space it is possible to exactly represent a signed integer of any size, but we can usually get by with numbers less than 2 billion.

The internal mechanics of counting with signed integers are the same as with unsigned integers, except for the mapping of the largest unsigned values to the negative part of the range. As a result, signed integers wrap around from a large positive value to a large negative value and run continuously through zero from negative to positive just as one would expect.

Integer Division

Just as addition and multiplication may result in an overflow beyond the limits of the storage format and wrap around, integer division may result in a remainder, that would be expressed as a fraction. That fraction is truncated in most languages, with the result that 3/2 yields 1, while 3.0/2.0 yields 1.5. A notable exception is Python version 3 and above where 4/2 results in an integer 2, but 3/2 results in a floating point value of 1.5

Floating Point Numbers

Most engineering calculations require lots of Real Numbers, large or small, positive or negative, rational (expressible in a finite number of digits) or irrational like . Floating point numbers allow the decimal point to move around by being composed of a mantissa and an exponent, all packaged into a fixed size format with limits on the size of the number arising in the same way as for signed and unsigned integers.

Wikipedia provides more detail on number formats than you are ever likely to need. The single precision pages show how real numbers are represented in 32 bits to cover a range of about +- 3.4E38 with about 7 decimal digits of accuracy. Because all of the actual arithmetic takes place in base 2, the translation to limits in decimal numbers is only approximate.

Because a single precision number packs both mantissa and exponent into 32 bits, there are integer values that can be exactly represented by a 32 bit integer number that can only be approximated by a single precision floating point number. Counting to a billion in single precision will fail along the way.

Double precision numbers use 64 bits to provide about 16 decimal digits of accuracy over a range of and should be your default choice to avoid roundoff errors.

There are some special results you can get from floating point calculations:

• NaN – Not a Number results from things like the square root of a negative number that are just not defined for real numbers.
• +infinity, -infinity – usually result from division by zero
• overflow, underflow – too big or too small to be represented, but finite

If one of these shows up in your output you have probably made a coding error.

Choosing a Format for your Numbers

Often the format is chosen for you and this can make your life a lot easier. With choice comes power and the power to really screw things up with a bad choice comes along with the power to make things faster, more space efficient, and elegant with a good choice.

ANSI C and Arduino

The size of unsigned and int, both short and long, will depend on the processor and the compiler, so be careful if you will depend on boundary behaviours of 16 or 32 bit numbers. This allows the compiler to be optimized for the hardware, as 16 bit memory access and calculation may actually be less efficient than 32 bit if that is the native size of the processor registers and memory pathways. If you need to know for sure, use the sizeof(x) function to find out how many bytes are used to represent the variable x in storage, or use types of int8_t, int16_t, int32_t, uint8_t, uint16_t, uint32_t for signed and unsigned integers of exactly a specific size.

long long int and long long unsigned are available on larger processors to provide a 64 bit integer type with values up to more than .

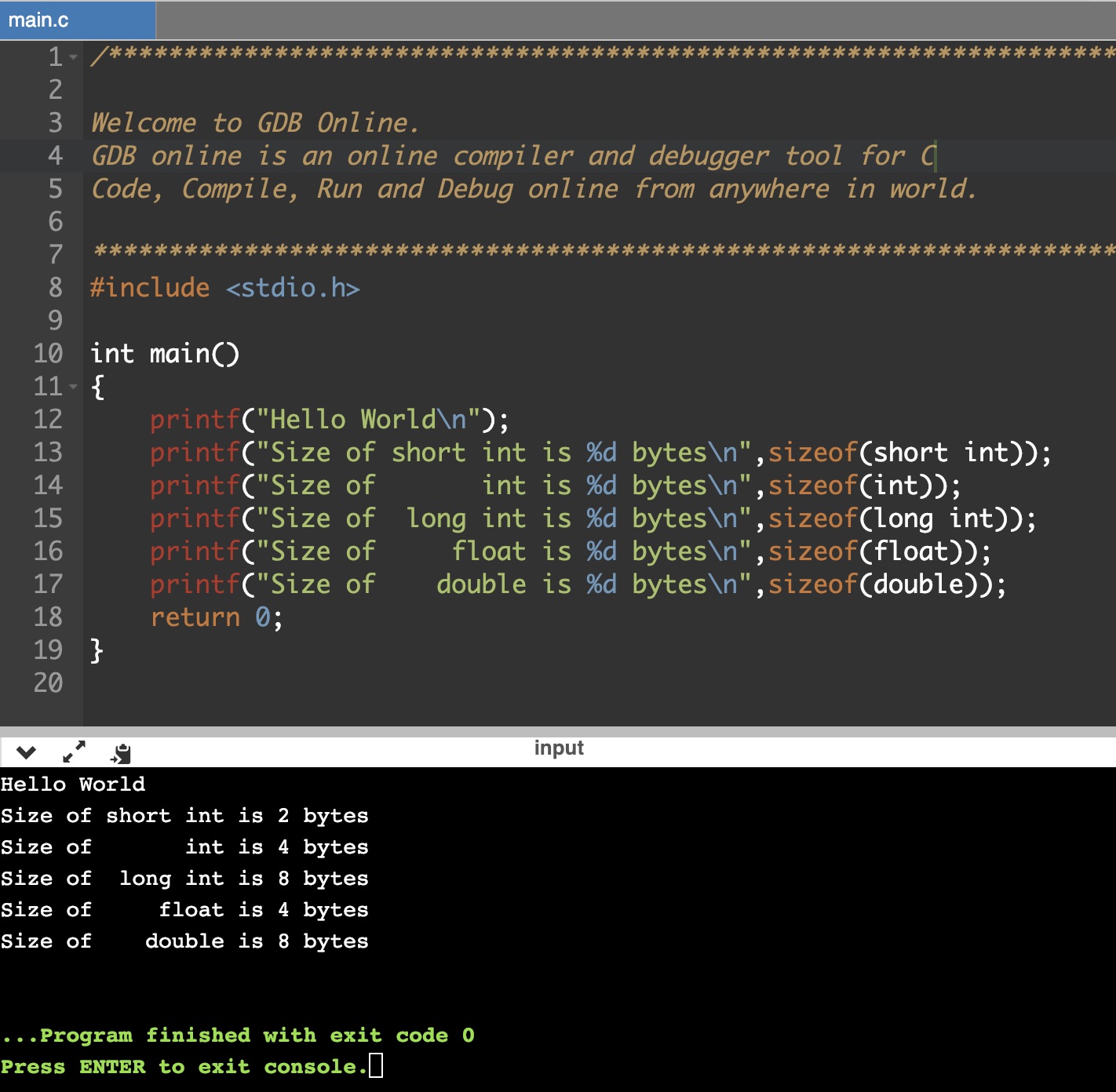
Use unsigned long to keep track of time. Time goes only forward, so the elapsed time since a machine was turned on, or since 1970-01-01 will always be positive and it could make sense to express time as an unsigned long in either seconds since 1970-01-01 (136 years between rollovers of the unix epoch) or the number of microseconds since the microcontroller restarted (71.6 minutes before rollover of the Arduino micros( ) function). Both of these simple time counters have the advantage that the difference between two values will always be the elapsed time, as long as the time between the values doesn’t cross more than one rollover.

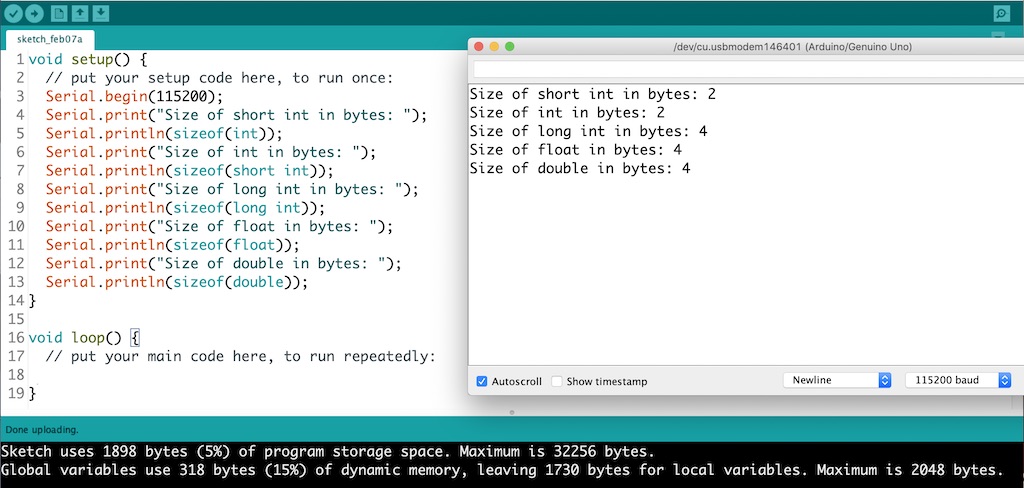
Use int for counters and array indices, and anything where you might be subtracting. Unless of course you are going to use really big arrays and need to count over 30,000, when you would explicitly use a long int. Unsigned values make sense as indices, but can yield some funny results if you take the difference between two indices. Larger – smaller will be correctly small and positive, but smaller – larger will be an enormous positive value instead of a small negative value. int is safer.

Use long int for sums unless you know they will be small. Adding together multiple short values to take an average will very quickly overflow and yield confusing results.

Use double for all your real numbers. This is the default in C and makes sense unless you are really pushed for memory space. A float takes half as much space as a double. Beware that some Arduino variants like the UNO use 8 bit processors and support only float. Declarations of double on the UNO are automatically reduced to float without producing a warning.

Reduce storage size only if you need too! Leaving memory empty doesn’t gain you much, and overflow and rounding errors can be really hard to diagnose. Smaller number formats can result in faster calculations, but this is much less of a factor in machines with 64 bit processors and data pathways. First make it work, then make it small and fast if you need to.  Some microcontrollers provide only 32 bit floating point processors, making float operations significantly faster than double. You will probably need to think carefully about space on an Arduino UNO with 2K of memory available for variable storage space. 2K is 2048 bytes, which is 1024 integers or 512 floats. The power of choice you get with C is essential in this limited environment!

Python

Python will choose number formats for you, either integers of unlimited size (starting with Python 3) or double precision floating point numbers whenever the result isn’t an integer. The only major complication is you will need to convert a floating point number back into an integer before you can use it as an array index. (Note that while Python native integers may be unlimited size, numpy integers are fixed size dependent on the implementation. The result of 300**4 will be incorrect on the Windows implementation of Python 3.8 because it uses 32 bit integers and overflows. The Mac implementation uses 64 bit integers and gets the correct value of 8,100,000,000.)

CircuitPython

Mostly the same as regular Python, with differences in floating point precision, and it does support unlimited size integers on Express boards, starting with CircuitPython v3. for more details see https://learn.adafruit.com/circuitpython-essentials/circuitpython-expectations

MATLAB(R)

Every number in MATLAB is a double precision floating point number.