B.1: Drawing Supertypes and Subtypes on the Red

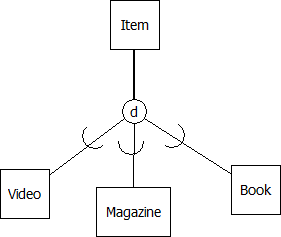
There are different ways that supertypes and subtypes can be shown on an ERD. We will continue with the Peter Chen notation in this appendix. Between a supertype and its subtypes we show a connection symbol (a circle) where one line is drawn from the supertype to the connection symbol and then lines are drawn from the connection symbol to each subtype.

A collection of related subtypes can be regarded as overlapping or disjoint. Subtypes are considered as disjoint if it is impossible for an instance of a supertype to be regarded as being an instance of more than one subtype. For example, a library item will be one and only one of its subtypes (magazine, video, book). Subtypes are considered as overlapping if it is possible for an instance of a supertype to be regarded as being an instance of more than one subtype. An example of overlapping can exist with people in a university environment: it is possible that some person could be both an employee and a student at the same time. In our Peter Chen notation, we will use a “d” in the connection symbol to represent disjoint subtyping, and we will use “o” to represent overlapping.

In our notation we also include an arc on each of the lines joining the connection symbol to the subtypes that implies “containment”.

To illustrate the drawing technique, consider a library where items are loaned to members and where an item can be either a video, a magazine, or a book, and suppose also that an item belongs to exactly one (i.e., disjoint subtypes) of these subtypes. We can show this as:

We extend our notation once more. To indicate that a supertype must exist as one of its subtypes we show total participation in subtyping by using a double line. For example, if we want to show that each item must be one of the subtypes:

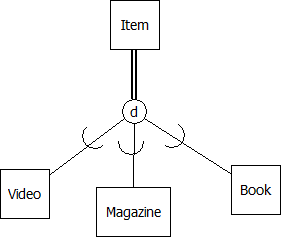
The double line from Item to the connection symbol shows total participation of Item in the subtyping: whenever there is an instance of an Item, then that item must also be one of the subtypes shown – a video, a magazine, or a book. If we did not specify total participation then we would be allowing an item to exist where that item is not a video, nor is it a magazine, nor is it a book. So, participation of a supertype in the subtyping is either total or optional. The converse is always true: if we have an instance of a subtype then that instance is an instance of the supertype. In the library model then, if we have an instance of book then that instance is of course an item.