10. NORMALIZATION
10.1: Functional Dependencies
To understand normalization theory (first, second, third and Boyce-Codd normal forms), we must understand what is meant by the term functional dependency. There is another type of dependency called a multi-valued dependency but that is important to the understanding of higher normal forms not covered in this text.
A functional dependency is an association between two attributes. We say there is a functional dependency from attribute A to an attribute B if and only if for each value of A there can be at most one value for B. We can illustrate this by writing:
-
-
- A functional determines B, or
- B is functionally determined by A, or
- by a drawing such as:
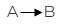
-
When we have a functional dependency from A to B, we refer to attribute A as the determinant.
EXAMPLE 1.
Consider a company collects information about each employee such as the employee’s identification number (ID), their first name, last name, salary and gender. As is typical, each employee is given a unique ID which serves to identify the employee. Hence for each value of ID there is at most one value for first name, last name, salary and gender.
Therefore, we have four functional dependencies where ID is the determinant; we can show this as a list or graphically:

If you think about this case, there cannot be any other FDs. For example, consider the gender attribute – we need to allow for more than one employee for a given gender, and so we cannot have a situation where gender functionally determines ID. So, gender ID cannot exist. Now consider the first name attribute. Again, we need to allow for more than one employee to have the same first name and so first name cannot determine anything. Similarly, for other attributes.
EXAMPLE 2.
Recall the Department and Course tables introduced in Chapter 2 – sample data is shown below:
|
deptCode |
deptName |
deptLocn |
deptPhone |
chairName |
|
MATH |
Mathematics |
2R33 |
786-0033 |
Peter Smith |
|
HIST |
History |
3D07 |
786-0300 |
Simon Lee |
|
IS |
Indigenous Studies |
3C11 |
786-3322 |
Leslie Roman |
|
MENN |
Mennonite Studies |
3C11 |
786-3322 |
Leslie Roman |
|
BIOL |
Biology |
2L88 |
786-9843 |
James Dunn |
|
deptCo de |
courseN o |
title |
description |
creditHou rs |
|
HIST |
1010 |
Introduction to History |
Within a relatively small lecture/seminar setting, this course introduces you to the ways in which people try to understand their present by studying their past. |
6 |
|
IS |
1010 |
Indigenous Ways of Knowing |
This course offers an introduction to Indigenous ways of knowing through active participation in strategies that facilitate the production of Aboriginal knowledge and through comparisons with Euro-American ways of knowing. |
3 |
|
MENN |
1010 |
Mennonites and the Modern World |
This course is a history of the ethnic identity and religious faith of the Mennonites from the sixteenth century to the present. |
6 |
|
IS |
1201 |
Introductory Ojibwe |
This course is intended for students who are not fluent in Ojibwe and have never taken a course in the language |
6 |
|
BIOL |
2401 |
Forest Field Skills Camp |
This intensive two-week field course is mandatory for students in the Forest Ecology program and is designed to give students field survival and basic forestry skills. |
1 |
Recall the primary keys (underlined above) of these two tables:
|
Table |
PK |
|
Department |
deptCode |
|
Course |
deptCode, courseNo |
Consider the Department table where deptCode is the primary key. For each value of deptCode there is at most one value for deptName, deptLocn, deptPhone, and chairName. You should agree the following FDs exist:
-
-
- deptCode –> deptName
- deptCode –> deptLocn
- deptCode –> deptPhone
- deptCode –> chairName
-
Each row of the Course table has one value for title, one value for description, and one value for credit hours. The primary key of Course consists of two attributes, deptCode and courseNo. The following FDs exist for the Course table:
-
-
- deptCode, courseNo –> title
- deptCode, courseNo –> description
- deptCode, courseNo –> credit hours
-
In this case we have a determinant comprising two attributes; the determinant is composite.
We can draw the functional dependencies as:
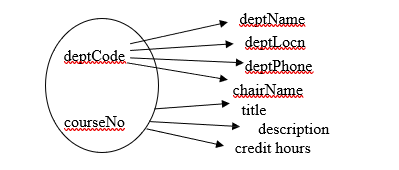
Could there be other functional dependencies in this situation?
These examples demonstrate that there is a FD from the primary key to each of the other attributes in a table.
EXAMPLE 3.
The following ERD is shown in the Chen notation. There is one entity type named Employee that has 4 attributes. In this design there are two keys (id and sin) and two descriptive attributes (firstName and lastName):
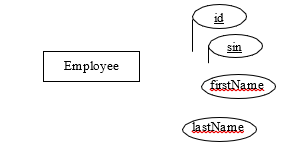
Each symbol in an ERD contains information about a model. From the above we know there are two keys, id and sin. An id value, or a sin value, will uniquely identify an employee and so we have the six FDs:
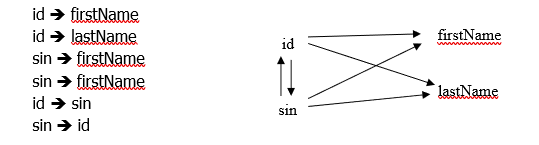
This example shows that an ERD carries information that can be expressed in terms of FDs.
Exercises
1) Consider the Product table below where productID is the PK. What FDs must exist in this table:
|
productID |
description |
unit price |
quantity on hand |
|
33 |
16 oz. can tomato soup |
1.00 |
50 |
|
41 |
454 grams box corn flakes |
4.50 |
39 |
|
45 |
Package red licorice |
1.00 |
39 |
|
46 |
Package black licorice |
1.00 |
50 |
|
47 |
1 litre 1% milk |
1.99 |
25 |
2) Consider the ERD where the entity type Employee has one key attribute, id, and the entity type Position has one key attribute, title. As well the ERD shows a one-to-many relationship assigned to which can be expressed as:
- An employee is assigned to at most one position. A position can be assigned to many employees.
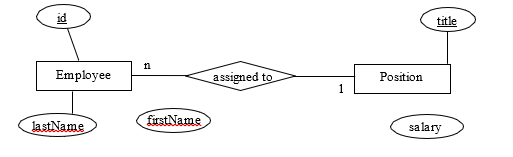
- List the FDs that must be present.
3) Consider the ERD below which is similar to the above, but where the assigned to relationship is many-to-many, and where assigned to has an attribute startDate. List the FDs that are present.
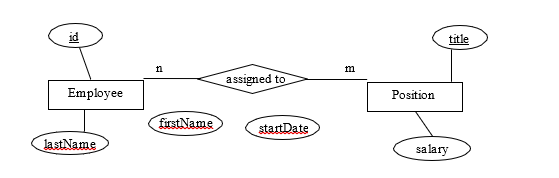
4) Consider the ERD below where Department has two keys deptCode and deptName – each department has a unique department code and has a unique department name. Course is a weak entity type with a partial key courseNo, and where offers is an identifying relationship.
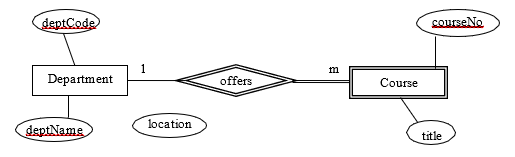
- List the FDs that must exist.
5) Consider the table T with attributes A, B and C.
|
A |
B |
C |
|
1 |
33 |
100 |
|
2 |
33 |
200 |
|
3 |
22 |
200 |
|
1 |
33 |
101 |
|
2 |
33 |
350 |
|
4 |
67 |
350 |
|
5 |
67 |
101 |
6) Suppose there are many more rows that are not shown:
- Is there a functional dependency from B to A? Explain your answer.
- The rows that are shown suggest there could be a functional dependency A –> B. Compose a database query that would indicate counter examples, if they exist, for the functional dependency A –> B. Such a query would list values of A in the table where two or more rows have the same value for A but different values for B.

